题目内容
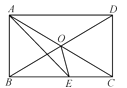
【题目】如图所示,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,垂足分别为E、F,且AB=CD.
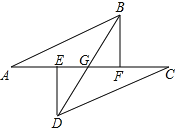
(1)△ABF与△CDE全等吗?为什么?
(2)求证:EG=FG.
【答案】(1)△ABF与△CDE全等,理由见解析;(2)见解析.
【解析】
(1)由AE=CF可得AF=CE,再用HL证明Rt△ABF≌Rt△CDE即可;
(2)先用AAS证明△DEG≌△BFG,再根据全等三角形的性质即得结论.
(1)解:△ABF与△CDE全等,理由如下:
∵DE⊥AC,BF⊥AC,
∴∠AFB=∠CED=90°,
∵AE=CF,
∴AE+EF=CF+EF,即AF=CE,
在Rt△ABF和Rt△CDE中,![]() ,
,
∴Rt△ABF≌Rt△CDE(HL);
(2)证明:∵Rt△ABF≌Rt△CDE,
∴BF=DE,
在△DEG和△BFG中, ,
,
∴△DEG≌△BFG(AAS),
∴EG=FG.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目