Question

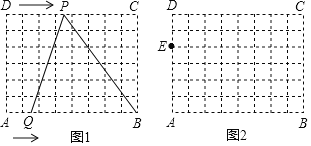
【题目】如图，已知△ABC是等腰直角三角形，AB=AC，AD是斜边的中线，E、F分别是AB、AC边上的点且DE⊥DF.

（1）求证:△AED≌△CFD；

（2）若BE=8，CF=6，求△DEF的面积；

（3）若AB=a，AE=x，请用含x，a的代数式表示△DEF的面积S.

Answer 1

【答案】见解析

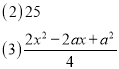
【解析】

（1）由△ABC是等腰直角三角形，AB=AC，AD是斜边的中线，可得：AD=DC，∠EAD=∠C=45°，AD⊥BC即∠CDF+∠ADF=90°，又DE⊥DF，可得：∠EDA+∠ADF=90°，故∠EDA=∠CDF，从而可证：△AED≌△CFD；

（2）由（1）知：AE=CF，AF=BE，DE=DF，即△EDF为等腰直角三角形，在Rt△AEF中，运用勾股定理可将EF的值求出，进而可求出DE、DF的值，

（3），由，可解.

∵ABC是等腰直角三角形，AD是斜边的中线，

∴AD=AC,EAD=C=45 ,ADBC,

∴CDF+ADF=90,

又DEDF, ∴EDA+ADF=90,故EDA=CDF，

在AED和CFD中 ,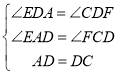

∴△AED≌△CFD .

(2)由（1）知：AE=CF,AF=BE,DE=DF,即△EDF为等腰直角三角形，在Rt△AEF中，EF=

∴DE2+DF2=102 ∴DE=DF=

∴ .

(3)AF=BE=a-x , AE=CF=x ,

DE2 == ,

∴EDF= DE2= = = .