题目内容
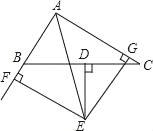
【题目】如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,BE平分∠ABC交AC于E,交AD于F,FG∥BC,FH∥AC,下列结论:①AE=AF;②AF=FH;③AG=CE;④AB+FG=BC,其中正确的结论有________________.(填序号)

【答案】①②③④
【解析】
①正确.
∵∠BAC=90°
∴∠ABE+∠AEB=90°
∴∠ABE=90°-∠AEB
∵AD⊥BC
∴∠ADB=90°
∴∠DBE+∠BFD=90°
∴∠DBE=90-∠BFD
∵∠BFD=∠AFE
∴∠DBE=90°-∠AFE
∵BE平分∠ABC
∴∠ABE=∠DBE
∴90°-∠AEB=90°-∠AFE
∴∠AEB=∠AFE
∴AE=AF
②正确.
∵∠BAC=90°
∴∠BAF+∠DAC=90°
∴∠BAF=90°-∠DAC
∵AD⊥BC
∴∠ADC=90°
∴∠C+∠DAC=90°
∴∠C=90°-∠DAC
∴∠C=∠BAF
∵FH∥AC
∴∠C=∠BHF
∴∠BAF=∠BHF
在△ABF和△HBF中
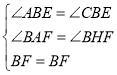
∴△ABF≌△HBF
∴AF=FH
③正确.
∵AE=AF,AF=FH
∴AE=FH
∵FG∥BC,FH∥AC
∴四边形FHCG是平行四边形
∴FH=GC
∴AE=GC
∴AE+EG=GC+EG
∴AG=CE
④正确.
∵四边形FHCG是平行四边形
∴FG=HC
∵△ABF≌△HBF
∴AB=HB
∴AB+FG=HB+HC=BC
故正确的答案有①②③④.

练习册系列答案
相关题目