题目内容
【题目】如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠P=20°,∠D=100°,则∠C=______°.
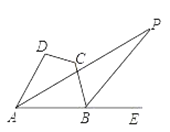
【答案】120
【解析】
利用四边形内角和是360°可以求得∠DAB+∠ABC=360°-∠C-∠D.然后由角平分线的性质及邻补角的定义求得∠PAB+∠ABP=![]() ∠DAB+∠ABC+
∠DAB+∠ABC+![]() (180°-∠ABC)=90°+
(180°-∠ABC)=90°+![]() (∠DAB+∠ABC),由三角形内角和得∠PAB+∠ABP=180°-∠P,由以上两式可求出∠C的度数.
(∠DAB+∠ABC),由三角形内角和得∠PAB+∠ABP=180°-∠P,由以上两式可求出∠C的度数.
如图,∵∠DAB+∠ABC+∠C+∠D=360°,
∴∠DAB+∠ABC=360°-∠C-∠D.
又∵∠DAB的角平分线与∠ABC的外角平分线相交于点P,
∴∠PAB+∠ABP=![]() ∠DAB+∠ABC+
∠DAB+∠ABC+![]() (180°-∠ABC)
(180°-∠ABC)
=90°+![]() (∠DAB+∠ABC)
(∠DAB+∠ABC)
=90°+![]() (360°-∠C-∠D)
(360°-∠C-∠D)
=270°-![]() ∠C-∠
∠C-∠![]() D,
D,
∵∠PAB+∠ABP=180°-∠P,
∴270°-![]() ∠C-∠
∠C-∠![]() D=180°-∠P,
D=180°-∠P,
∴270°-![]() ∠C-
∠C-![]() ×100°=180°-20°,
×100°=180°-20°,
∴∠C=120°
故答案为120°.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目





