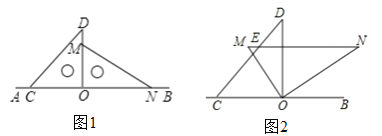题目内容
【题目】如图,△ABC中,AB=AC,△ABD和△ACE分别是以AB、AC为斜边的等腰直角三角形,BE、CD相交于点F.求证:AF⊥BC.

【答案】见解析
【解析】
先证明△ABD≌△ACE,从而有DB=CE,接着证明△DBC≌△ECB,从而∠DCB=∠EBC,所以FB=FC,所以F在BC的垂直平分线上,另A点在BC垂直平分线上,所以AF⊥BC.
证:在△ABD和△ACE中,
∵AB=AC,∠ABD=∠ACE,DB=EC,
∴△ABD≌△ACE.
∴DB=EC.
在△DBC和△ECB中,
∵DB=EC,∠DBC=∠ECB,BC=CB,
∴△DBC≌△ECB.
∴∠DCB=∠EBC,
∴FB=FC.
∴F在BC的垂直平分线上.
又∵另A点在BC垂直平分线上,
∴AF⊥BC.

练习册系列答案
相关题目