题目内容
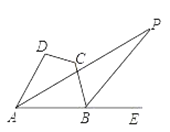
【题目】如图,BC=2,A为半径为1的⊙B上一点,连接AC,在AC上方作一个正六边形ACDEFG,连接BD,则BD的最大值为 . 
【答案】![]()
【解析】解:∵六边形ACDEFG是正六边形,
∴AC=CD,∠ACD=(6﹣2)×180°÷6=120°,
把△ABC和⊙B绕点C旋转120°得△DHC和⊙H,BH的延长线与⊙H的交点为M,
作CN⊥BM于N,如图所示:

则BM的长度就是DB达到的最大值,∠BCH=120°,CH=CB=2,BN=HN,
∴∠B=∠CHB=(180°﹣120°)÷2=30°,
∴CN= ![]() BC=1,
BC=1,
∴BN= ![]() =
= ![]() ,
,
∴BH=2BN=2 ![]() ,
,
∴BM=BH+HM=2 ![]() +1,
+1,
即BD的最大值为2 ![]() +1,
+1,
所以答案是:2 ![]() +1.
+1.
【考点精析】关于本题考查的正多边形和圆,需要了解圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角;圆的外切四边形的两组对边的和相等才能得出正确答案.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
【题目】某校计划成立学生社团,要求每一位学生都选择一个社团,为了了解学生对不同社团的喜爱情况,学校随机抽取了部分学生进行“我最喜爱的一个学生社团”问卷调查,规定每人必须并且只能在“文学社团”、“科学社团”、“书画社团”、“体育社团”和“其他”五项中选择一项,并将统计结果绘制了如下两个不完整的统计图表.
社团名称 | 人数 |
文学社团 | 18 |
科技社团 | a |
书画社团 | 45 |
体育社团 | 72 |
其他 | b |
请解答下列问题:
(1)a= , b=;
(2)在扇形统计图中,“书画社团”所对应的扇形圆心角度数为;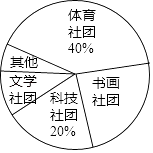
(3)若该校共有3000名学生,试估计该校学生中选择“文学社团”的人数.