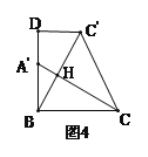ĢāÄæÄŚČŻ
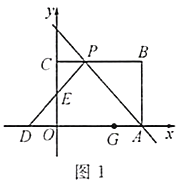
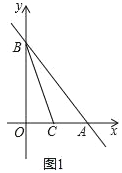
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µćOĪŖ×ų±źŌµć£¬Ö±Ļßy=©![]() x+12ÓėxÖį£¬yÖį·Ö±šĻą½»ÓŚµćA£¬B£¬”ĻABOµÄĘ½·ÖĻßÓėxÖįĻą½»ÓŚµćC£®
x+12ÓėxÖį£¬yÖį·Ö±šĻą½»ÓŚµćA£¬B£¬”ĻABOµÄĘ½·ÖĻßÓėxÖįĻą½»ÓŚµćC£®
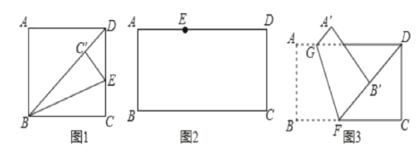
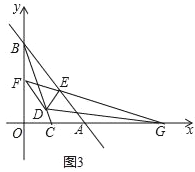
£Ø1£©ČēĶ¼1£¬ĒóµćCµÄ×ų±ź£»
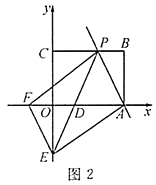
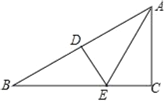
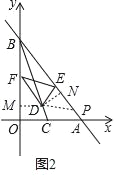
£Ø2£©ČēĶ¼2£¬µćD£¬E£¬F·Ö±šŌŚĻ߶ĪBC£¬AB£¬OBÉĻ£ØµćD£¬E£¬F¶¼²»ÓėµćBÖŲŗĻ£©£¬Į¬½ÓDE£¬DF£¬EF£¬ĒŅ”ĻEDF+”ĻOBC=90”ć£¬ĒóÖ¤£ŗ”ĻFED=”ĻAED£»
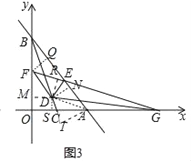
£Ø3£©ČēĶ¼3£¬ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬ŃÓ³¤Ļ߶ĪFEÓėxÖįĻą½»ÓŚµćG£¬Į¬½ÓDG£¬Čō”ĻCGD=”ĻFGD£¬BF£ŗBE=5£ŗ8£¬ĒóÖ±ĻßDFµÄ½āĪöŹ½£®

”¾“š°ø”æ£Ø1£©µćC×ų±źĪŖ£Ø4£¬0£©£»£Ø2£©¼ū½āĪö£»£Ø3£©Ö±ĻßDFµÄ½āĪöŹ½ĪŖy=©![]() x+7£®
x+7£®
”¾½āĪö”æÕūĢå·ÖĪö£ŗ
£Ø1£©×÷CH”ĶABÓŚH£¬ÓÉ”÷OBC”Õ”÷HBCĒóBH£¬½āRt”÷ACH£¬ĒóCH£¬¼“µĆOC£»£Ø2£©¹żµćD·Ö±š×÷DM”ĶyÖįÓŚµćM£¬DN”ĶABÓŚµćN£¬ŌŚNAÉĻ½ŲČ”NP=FM£¬Į¬½ÓPD£¬ÓĆSASÖ¤”÷DFM”Õ”÷DPN£¬µĆDF=DP£¬”ĻEDF=”ĻEDP£¬Ö¤”÷DEF”Õ”÷DEP£»£Ø3£©¹żµćF×÷FQ”ĶBEÓŚµćQ£¬¹żµćD×÷DM”ĶyÖįÓŚM£¬DN”ĶABÓŚN£¬DR”ĶEFÓŚR£¬DS”ĶOGÓŚµćS£¬¹żµćA×÷AT”ĶBC½»BCµÄŃÓ³¤ĻßÓŚT£¬Į¬½ÓAD£®½āRt”÷ACTĒóST£¬AT£¬”ĻADT=”ĻDAT=45”ć£¬ĒóDC£¬“Ó¶ųµĆDS£¬OS£¬Ēó³öDµÄ×ų±ź£¬ÅŠ¶ĻDF”ĪAB£¬¼“æÉĒóDFµÄ½āĪöŹ½.
½ā£ŗ£Ø1£©ČēĶ¼1£¬×÷CH”ĶABÓŚH£®

ÓÉĢāŅāA£Ø9£¬0£©£¬B£Ø0£¬12£©£¬
ŌŚRt”÷AOBÖŠ£¬AB=![]() =
=![]() =15£¬tan”ĻOAB=
=15£¬tan”ĻOAB=![]() =
=![]() =
=![]() £¬
£¬
”ß”ĻCBH=”ĻCBO£¬”ĻCHB=”ĻCOB£¬CB=CB£¬
”ą”÷OBC”Õ”÷HBC£¬
”ąBH=OB=12£¬OC=CH£¬AH=15©12=3£¬
ŌŚRt”÷ACHÖŠ£¬tan”ĻCAH=![]() =
=![]() £¬
£¬
”ĻCH=4£¬
”ąOC=CH=4£¬
”ąµćC×ų±źĪŖ£Ø4£¬0£©£®
£Ø2£©½ā£ŗČēĶ¼2£¬¹żµćD·Ö±š×÷DM”ĶyÖįÓŚµćM£¬DN”ĶABÓŚµćN£¬ŌŚNAÉĻ½ŲČ”NP=FM£¬Į¬½ÓPD£®
”ß”ĻEDF+”ĻOBC=90”ć£¬”ĻBDM+”ĻOBC=90”ć£¬
”ą”ĻEDF=”ĻBDM£¬Ķ¬Ąķ”ĻBDN=”ĻBDM=![]() ”ĻMDN£¬
”ĻMDN£¬
”ą”ĻEDF=![]() ”ĻMDN£¬
”ĻMDN£¬
”ß”ĻDBM=”ĻDBN£¬DM”ĶOB£¬DN”ĶAB£¬
”ąDM=DN£¬
”ß”ĻFMD=”ĻPND=90”ć£¬NP=FM£¬
”ą”÷DFM”Õ”÷DPN£¬
”ąDF=DP£¬”ĻFDM=”ĻPDN£¬
”ą”ĻFDM+”ĻFDN=”ĻPDN+”ĻFDN£¬¼“”ĻFDP=”ĻMDN£¬
”ą”ĻEDF=![]() ”ĻFDP=”ĻEDP£¬
”ĻFDP=”ĻEDP£¬
”ßDE=DE£¬
”ą”÷DEF”Õ”÷DEP£¬
”ą”ĻFED=”ĻAED£®
£Ø3£©½ā£ŗČēĶ¼3£¬¹żµćF×÷FQ”ĶBEÓŚµćQ£¬¹żµćD×÷DM”ĶyÖįÓŚM£¬DN”ĶABÓŚN£¬DR”ĶEFÓŚR£¬DS”ĶOGÓŚµćS£¬¹żµćA×÷AT”ĶBC½»BCµÄŃÓ³¤ĻßÓŚT£¬Į¬½ÓAD£®
”ß”ĻDEF=”ĻDEA£¬DR”ĶEF£¬DN”ĶEA£¬
”ąDR=DN£¬Ķ¬ĄķDR=DS£¬
”ąDN=DS£¬
”ą”ĻBAD=”ĻOAD£¬Ķ¬Ąķ”ĻOFD=”ĻDFG£¬
ŌŚRt”÷ACTÖŠ£¬AC=9©4=5£¬tan”ĻACT=tan”ĻBCO=![]() =3£¬
=3£¬ ![]() =3£¬
=3£¬
ÉčCT=m£¬ŌņAT=3m£®
”ßCT2+AT2=AC2£¬
”ąm2+£Ø3m£©2=52£¬
½āµĆm=![]() »ņ©
»ņ©![]() £ØÉį£©£¬
£ØÉį£©£¬
”ąCT=![]() £¬AT=
£¬AT=![]() £¬
£¬
”ß”ĻADC=”ĻABD+”ĻBAD=![]() £Ø”ĻOBA+”ĻBAO£©=
£Ø”ĻOBA+”ĻBAO£©=![]() ”Į90”ć=45”ć£¬
”Į90”ć=45”ć£¬
”ą”ĻDAT=45”ć=”ĻADC£¬
”ąDT=AT=![]() £¬
£¬
”ąCD=DT©CT=![]() £¬Ķ¬ĄķæÉµĆ£¬CS=1£¬DS=3=OM£¬
£¬Ķ¬ĄķæÉµĆ£¬CS=1£¬DS=3=OM£¬
”ąOS=4©1=3£¬
”ąµćD×ų±ź£Ø3£¬3£©£¬
ÉčBF=5n£¬ŌņBE=8n£¬ŌŚRt”÷BFQÖŠ£¬cos”ĻFBQ=![]() =
=![]() =
=![]() £¬
£¬
”ąBQ=4n=EQ£¬
”ąFQ”ĶAB£¬”ĻBFQ=”ĻEFQ£¬
”ą”ĻDFQ=”ĻDFC+”ĻEFQ=![]() £Ø”ĻOFG+”ĻBFE£©=
£Ø”ĻOFG+”ĻBFE£©=![]() ”Į180”ć=90”ć£¬
”Į180”ć=90”ć£¬
”ą”ĻDFQ=”ĻBQF=90”ć£¬
”ąDF”ĪAB£¬
ÉčÖ±ĻßDFµÄ½āĪöŹ½ĪŖy=©![]() x+b£¬
x+b£¬
”ą3=©![]() ”Į3+b£¬
”Į3+b£¬
½āµĆb=7£¬
”ąÖ±ĻßDFµÄ½āĪöŹ½ĪŖy=©![]() x+7£®
x+7£®