��Ŀ����
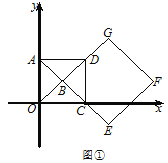
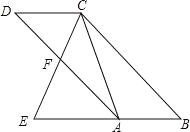
����Ŀ��(1)��ͼ1��������ABCD�۵���ʹBC���ڶԽ���BD�ϣ��ۺ�ΪBE����C���ڵ�C'��������ADB=46�������DBE�Ķ���Ϊ______.
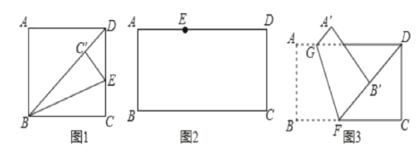
(2)С��������һ�ž���ֽƬABCD��AB=4��AD=9��
����һ����
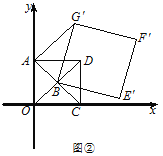
��ͼ2����E�����ž���ֽƬ�ı�AD�ϣ���ֽƬ�۵���ʹAB����CE����ֱ���ϣ��ۺ���ΪMN(��M��N�ֱ��ڱ�AD��BC��)������ֱ�ߺ�Բ�滭���ۺ�MN(��д������������ͼ�ۼ������ú�ɫˮ�ʰ��߶������)��
����һ�㣩
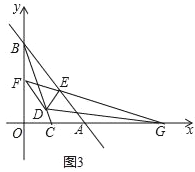
��ͼ3����F�����ž���ֽƬ�ı�BC�ϣ���ֽƬ�۵���ʹFB��������FD�ϣ��ۺ�ΪGF����A��B�ֱ����ڵ�A'��B'������AG=![]() ����B'D�ij���
����B'D�ij���
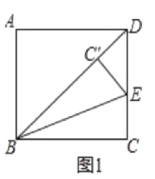
���𰸡�(1)23(2)����һ������ͼ������;����һ�㡿DB`=3
��������
(1)���ݾ������ʿɵ�AD��BC,�Ӷ��ɵá�ADB=��DBC=46��,�ٸ��ݷ��۵����ʼ�����á�DBE�Ķ�
(2)��һ��:����CE���ӳ���BA���ӳ������G,���ó߹���ͼ������BGC�Ľ�ƽ�����ɵ�ץ��MN,
��һ��:����֪�ɵ�GD=![]() ,���ݾ��ε����ʼ����۵����ʿɵá�DFG=��DGF,�Ӷ��ɵ�DF=DG=
,���ݾ��ε����ʼ����۵����ʿɵá�DFG=��DGF,�Ӷ��ɵ�DF=DG=![]() ,��Rt��CDE��,���ݹ��ɶ��������CF=
,��Rt��CDE��,���ݹ��ɶ��������CF=![]() ,����BF=BC-CF���BF�ij�,�ٸ��ݷ��۵����ʼ̶������DB`�ij�����
,����BF=BC-CF���BF�ij�,�ٸ��ݷ��۵����ʼ̶������DB`�ij�����
(1)��ͼ1�У�
���ı���ABCD�Ǿ��Σ�
��AD//BC��
���ADB=��DBC=46����
�ɷ��۲����Կ�֪����DBE=��EBC=![]() ��DBC=23����
��DBC=23����
�ʴ�Ϊ23��
(2)����һ��������ͼ2�У�

����һ�㡿
��ͼ3�У�
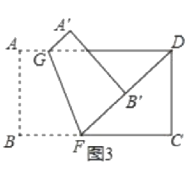
��AG=![]() ��AD=9��
��AD=9��
��GD=9![]() =
=![]() ��
��
���ı���ABCD�Ǿ��Σ�
��AD//BC��
���DGF=��BFG��
�ɷ��۲����Կ�֪����BFG=��DFG��
���DFG=��DGF��
��DF=DG=![]() ��
��
��CD=AB=4����C=90����
����Rt��CDF��CF=![]() ��
��
��BF=BCCF=![]() ��
��
�ɷ��۲����Կ�֪��FB=FB'=![]() ��
��
��DB'=DFFB'=![]()
![]() =3��
=3��