题目内容
【题目】已知Rt△ABC中,∠C=90°.
(1)已知 a=4![]() , b=2
, b=2![]() ,求 c ;
,求 c ;
(2)已知∠A=60°, c=2![]() +4,求 b ;
+4,求 b ;
(3)已知 a =10, c =10![]() ,求∠B;
,求∠B;
(4)已知 b =35,∠A=45°,求 a .
【答案】(1)2![]() (2)2+
(2)2+![]() (3)45°(4)35
(3)45°(4)35
【解析】整体分析:
(1)已知两直角边,求斜边,用勾股定理;(2)已知锐角,斜边,求邻边,用余弦;(3)已知斜边,邻边,求锐角,用余弦;(4)已知锐角,邻边求对边用正切.
解:(1)由勾股定理,得c=![]() =2
=2![]() .
.
(2)∵cosA=![]() ,∴b=ccosA=(
,∴b=ccosA=(![]() +4)cos60°=2+
+4)cos60°=2+![]() .
.
(3)∵cosB=![]() =
=![]() =
=![]() ,∴∠B=45°.
,∴∠B=45°.
(4)∵tanA=![]() ,∴a=btanA=35tan45°=35.
,∴a=btanA=35tan45°=35.

【题目】如图,在正方形ABCD中,P是对角线AC上一点(不与点A、C重合),连接PD,过点P作PE⊥PD交射线BC于点E.
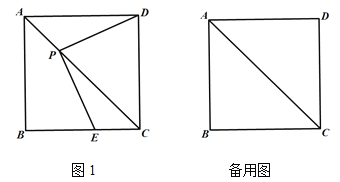
(1)如图1,求证:PD=PE;
(2)若正方形ABCD的边长为4,![]() ,求CE长.
,求CE长.
【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
1 | ° | x | 7 | ﹣3 | … |
(1)可知x= ,= ,°= ;
(2)试判断第2016个格子中的数是多少?并给出相应的理由.
(3)判断:前n个格子中所填整数之和是否可能为2016?若能,求出n的值,若不能,请说明理由.
【题目】某中学为筹备校庆活动,准备印刷一批校庆纪念册,该纪念册每册需要10张同样大小的纸,其中4张为彩页,6张为黑白页,印制该纪念册的总费用由制版费和印刷费两部分组成,制版费与印数无关,价格为彩页300元/张,黑白页50元/张,印刷费与印数的关系见下表:
印数 |
|
|
彩色(单位:元/张) | 2.2 | 2.0 |
黑白(单位:元/张) | 0.7 | 0.6 |
求:(1)印刷这批纪念册的制版费为多少元?
(2)若印刷2千册,则共需多少费用?
(3)如果该校希望印数![]() 至少为4千册,总费用为
至少为4千册,总费用为![]() 元,请用含有
元,请用含有![]() 的式子表示总费用?
的式子表示总费用?