题目内容
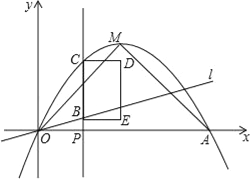
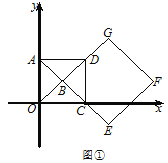
【题目】如图，矩形
摆放在平面直角坐标系中，点
在
轴上，点
在
轴上，
，
，过点的直线交矩形的边
于点
，且点不与点
、重合，过点作
，
交轴于点
，交轴于点
.
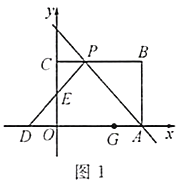
（1）如图1，若
为等腰直角三角形，求直线
的函数解析式；
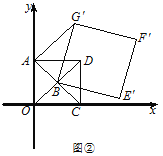
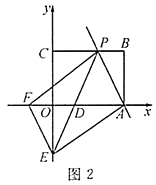
（2）如图2，过点作
交轴于点
，若四边形
是平行四边形，求直线
的解析式.
【答案】（1）
；（2）
.
【解析】
(1)先求得点P点坐标（1，2），再代入解析式y=kx+b,即可得出答案.
（2）作PM⊥AD于M,根据平行四边形性质求得点E和点P的坐标，再代入y=mx+n的解析式，即可得出答案.
解：（1）
矩形
,
，
，
A（3，0）B(3,2) C(0,2)
∠B=90°，CO=AB=2
为等腰直角三角形
P（1，2）
设直线
的函数解析式为
，过点A,点P
解k=-1,b=3
故直线的函数解析式为
（2）
作PM⊥AD于M
BC∥OA
∠CPD=∠PDA=∠APB
PD=PA,PM⊥AD
DM=AM
四边形PAEF是平行四边形
PD=DE
∠PMD=∠DOE,∠ODE=∠PDM
三角形PMD和三角形ODE全等
OD=DM=MA
OE=2,OM=2
E(0,2),P(2,2)
设直线PE的解析式为y=mx+n
解得m=2，n=-2
故直线PE的解析式为.
练习册系列答案
相关题目
