题目内容
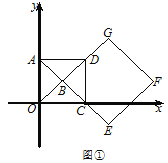
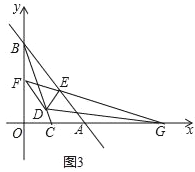
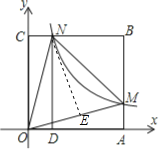
【题目】如图,在直角坐标系中,正方形OABC的顶点O与原点重合,顶点A,C分别在x轴,y轴上,反比例函数的图象与正方形的两边AB,BC分别交于点M,N,ND⊥x轴,垂足为D,连接OM,ON,MN.下列结论:①△OCN≌△OAM;②ON=MN;③四边形DAMN与△MON面积相等;④若∠MON=45°,MN=2,则点C的坐标为(0, ![]() +1).其中正确结论的序号是____________.
+1).其中正确结论的序号是____________.

【答案】①③④
【解析】试题解析:设反比例函数的解析式为: ![]()
∵点M、N都在![]() 的图象上,
的图象上,
∴![]() 即
即![]()
∵四边形ABCO为正方形,
∴![]()
∴NC=AM,
∴△OCN≌△OAM, ∴①正确;
∵△OCN≌△OAM,∴ON=OM,
∵k的值不能确定,
∴∠MON的值不能确定,
∴△ONM只能为等腰三角形,不能确定为等边三角形,
∴ON≠MN,
∴②错误;
∵![]()
而S△OND+S四边形DAMN=S△OAM+S△OMN,
∴四边形DAMN与△MON面积相等,
∴③正确;
作NE⊥OM于E点,如图所示:
∵![]() ,∴△ONE为等腰直角三角形,
,∴△ONE为等腰直角三角形,
∴NE=OE,
设NE=x,则![]()
∴![]()
∴![]()
在Rt△NEM中,MN=2,
∵![]() 即
即![]()
∴![]()
∴![]()
∵CN=AM,CB=AB,
∴BN=BM,
∴△BMN为等腰直角三角形,
∴![]()
设正方形ABCO的边长为a,则![]()
在Rt△OCN中, ![]()
∴![]() 解得
解得![]() (舍去),
(舍去),
∴![]()
∴C点坐标为![]()
∴④正确.
故答案为:①③④.

练习册系列答案
相关题目