题目内容
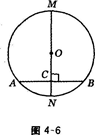
(本题8分)如图,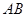 是⊙
是⊙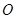 的切线,
的切线,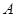 为切点,
为切点,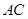 是⊙
是⊙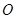 的弦,过
的弦,过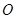 作
作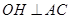 于点
于点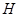 .若
.若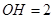 ,
,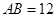 ,
,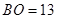 .
.
求:(1)⊙ 的半径;(2)AC的值.
的半径;(2)AC的值.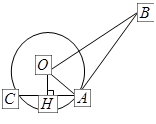
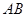 是⊙
是⊙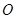 的切线,
的切线,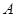 为切点,
为切点,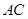 是⊙
是⊙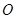 的弦,过
的弦,过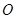 作
作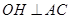 于点
于点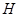 .若
.若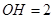 ,
,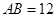 ,
,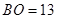 .
.求:(1)⊙
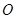 的半径;(2)AC的值.
的半径;(2)AC的值.
半径为5(4分); AC=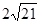 (4分)
(4分)
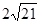 (4分)
(4分)分析:
①根据切线的性质可得△AOB是直角三角形,由勾股定理可求得OA的长,即⊙O的半径;
②在Rt△OAH中,由勾股定理可得AH的值,进而由垂径定理求得AC的长。
解答:
①∵AB是⊙O的切线,A为切点,
∴OA⊥AB,(1分)
在Rt△AOB中,
AO2= OB2-AB2=132-122=25
∴AO=5,
⊙O的半径为5;
②∵OH⊥AC,
∴在Rt△AOH中,
AH2= AO2-OH2=52-22=21
∴AH=
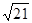
又∵OH⊥AC,
∴AC=2AH=2
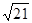
点评:此题考查的知识点有:切线的性质、全等三角形的判定和性质、勾股定理及垂径定理的综合运用等知识,需要特别注意的是:(1)题中,SSA不能作为判定三角形全等的依据。

练习册系列答案
相关题目
 ,则
,则 的度数为
的度数为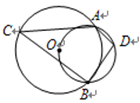
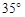
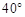
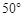
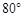
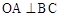 ,
,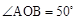 ,则
,则 的度数为( )
的度数为( )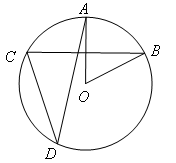
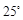
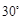
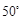
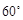
 为圆心,3cm为半径作⊙
为圆心,3cm为半径作⊙ 为圆心,2cm为半径作⊙
为圆心,2cm为半径作⊙