题目内容
已知⊙O的半径是5cm,弦AB∥CD,AB=6cm,CD=8cm则AB与CD的距是
1或7
分析:本题有两种情况,即AB,CD在圆心O的同侧或两侧两种情况,需分类讨论.
解:
: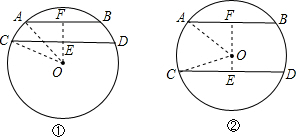
(1)如图①,过O作OF⊥AB于F交CD于E,连接OA,OC,
∵AB∥CD,∴OE⊥CD;
由垂径定理得AF=FB= AB=3,CE=DE=
AB=3,CE=DE= CD=4,
CD=4,
∴OF=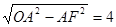 ,OE=
,OE=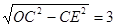
∴EF=OF-OE=1cm;
(2)过O作OF⊥AB于F,OE⊥CD于E,连接AO,CO,
同理可得OF=4cm,OE=3cm,
当AB,CD在圆心O的两侧时,
EF=OF+OE=7(cm),
∴AB与CD的距离为7cm或1cm.
点评:此题主要考查的是勾股定理及垂径定理的应用,需注意AB、CD的位置关系有两种,不要漏解.
解:
:

(1)如图①,过O作OF⊥AB于F交CD于E,连接OA,OC,
∵AB∥CD,∴OE⊥CD;
由垂径定理得AF=FB=
 AB=3,CE=DE=
AB=3,CE=DE= CD=4,
CD=4,∴OF=
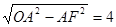 ,OE=
,OE=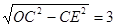
∴EF=OF-OE=1cm;
(2)过O作OF⊥AB于F,OE⊥CD于E,连接AO,CO,
同理可得OF=4cm,OE=3cm,
当AB,CD在圆心O的两侧时,
EF=OF+OE=7(cm),
∴AB与CD的距离为7cm或1cm.
点评:此题主要考查的是勾股定理及垂径定理的应用,需注意AB、CD的位置关系有两种,不要漏解.

练习册系列答案
相关题目
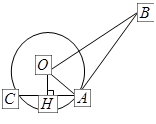
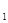 的半径为6cm,⊙O
的半径为6cm,⊙O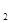 的半径是2cm,O
的半径是2cm,O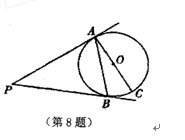
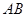 是⊙
是⊙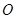 的切线,
的切线,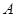 为切点,
为切点,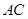 是⊙
是⊙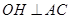 于点
于点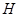 .若
.若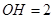 ,
,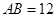 ,
,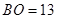 .
.
 O′交
O′交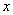 轴于D点,过点D作DF⊥AE于点F.
轴于D点,过点D作DF⊥AE于点F. 腰三角形,且点P一定在⊙O′外”.你同意他的看法吗?请充分说明理由.
腰三角形,且点P一定在⊙O′外”.你同意他的看法吗?请充分说明理由.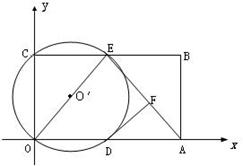
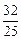 的k值?若存在,请求出符合的k值;若不存在,请说明理由。
的k值?若存在,请求出符合的k值;若不存在,请说明理由。