Question

【题目】海鲜门市的某种海鲜食材，成本为10元/千克，每天的进货量p（千克）与销售价格x（元/千克）满足函数关系式，从市场反馈的信息发现，该海鲜食材每天的市场需求量q（千克）与销售价格x（元/千克）满足一次函数关系，部分数据如下表：

销售价格x（元/千克）	10	12	…	30
市场需求量q（千克）	30	28	…	10

（已知按物价部门规定销售价格x不低于10元/千克且不高于30元/千克）

（1）请写出q与x的函数关系式：___________________________；

（2）当每天的进货量小于或等于市场需求量时，这种海鲜食材能全部售出，而当每天的进货量大于市场需求量时，只能售出符合市场需求量的海鲜食材，剩余的海鲜食材由于保质期短而只能废弃．

①求出每天获得的利润y（元）与销售价格x的函数关系式；

②为了避免浪费，每天要确保这种海鲜食材能全部售出，求销售价格为多少元时，每天获得的利润（元）最大值是多少？

Answer 1

【答案】（1）q=-x +40 ；(2)①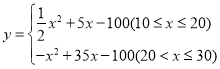；②销售价格为20元时，每天获得的利润最大值是200元

【解析】

（1）分析表中的变量关系可得q=-x +40；

（2）①分情况：，当时，；；当时，；

②要确保海鲜全部售出，所以p≤q，得，求函数最值可得.

解：（1）从表可得，q与x的函数关系式： q=-x +40

(2) ①，

当时，

，

当时，

综上所述：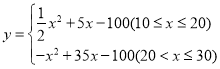

②要确保海鲜全部售出，所以p≤q

∴

∵，a>0，对称轴

∴当x=20时，y取最大值

（元）

答：销售价格为20元时，每天获得的利润最大值是200元.