题目内容
【题目】如图,在边长为![]() 的等边△ABC中,点D、E分别是边BC、AC上两个动点,且满足AE=CD. 连接BE、AD相交于点P,则线段CP的最小值为( )
的等边△ABC中,点D、E分别是边BC、AC上两个动点,且满足AE=CD. 连接BE、AD相交于点P,则线段CP的最小值为( )
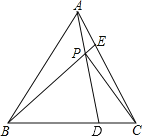
A.1B.2C.![]() D.
D.![]()
【答案】B
【解析】
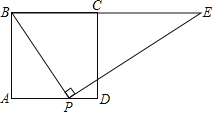
解:如图,

![]() ΔABC是等边三角形,
ΔABC是等边三角形,
![]() AB=BC=AC,∠ABC=∠BAC=∠BCE=
AB=BC=AC,∠ABC=∠BAC=∠BCE=![]() ,
,
![]() AE=CD
AE=CD![]() BD=CE,
BD=CE,![]() ΔABD≌ΔBCE(SAS)
ΔABD≌ΔBCE(SAS)
![]() ∠BAD=∠CBE,又
∠BAD=∠CBE,又![]() ∠APE=∠BAD+∠ABE,
∠APE=∠BAD+∠ABE,
![]() ∠APE=∠CBE+∠ABE=∠ABC,
∠APE=∠CBE+∠ABE=∠ABC,
![]() ∠APE=60°,
∠APE=60°,
![]() ∠APB=
∠APB=![]() ,
,
![]() 点P的运动轨迹是O为圆心,OA为半径的弧上运动,
点P的运动轨迹是O为圆心,OA为半径的弧上运动,
连接OC交⊙O于N,则OC⊥AB,
![]() 根据圆周角定理可得∠AOB=
根据圆周角定理可得∠AOB=![]() , ∠OAF=
, ∠OAF=![]() ,AF=
,AF=![]() AB=
AB=![]()
![]() OA=
OA=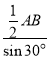 =2,
=2,
![]() OC=2OA=4
OC=2OA=4
当点P与N重合时,CP的值最小,最小值=OC-ON=4-2=2.
故选:B

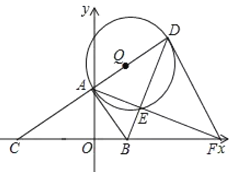
【题目】在等腰直角三角形![]() 中,
中,![]() ,
,![]() .点
.点![]() 为射线
为射线![]() 上一个动点,连接
上一个动点,连接![]() ,点
,点![]() 在直线
在直线![]() 上,且
上,且![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 的同侧,且
的同侧,且![]() ,连接
,连接![]() .请用等式表示线段
.请用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系.小明根据学习函数的经验.对线段
之间的数量关系.小明根据学习函数的经验.对线段![]() ,
,![]() ,
,![]() 的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:
的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:
(1)对于点![]() 在射线
在射线![]() 上的不同位置,画图、测量,得到了线段
上的不同位置,画图、测量,得到了线段![]() ,
,![]() ,
,![]() 的长度的几组值,如下表:
的长度的几组值,如下表:
位置 1 | 位置 2 | 位置 3 | 位置 4 | 位置 5 | 位置 6 | 位置 7 | 位置 8 | |
| 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 | 2.83 |
| 2.10 | 1.32 | 0.53 | 0.00 | 1.32 | 2.10 | 4.37 | 5.6 |
| 0.52 | 1.07 | 1.63 | 2.00 | 2.92 | 3.48 | 5.09 | 5.97 |
在![]() ,
,![]() ,
,![]() 的长度这三个量中,确定 的长度是自变量, 的长度是这个自变量的函数, 的长度是常量.
的长度这三个量中,确定 的长度是自变量, 的长度是这个自变量的函数, 的长度是常量.
(2)在同一平面直角坐标系![]() 中,画出(1)中所确定的函数的图象;
中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解决问题:请用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
【题目】海鲜门市的某种海鲜食材,成本为10元/千克,每天的进货量p(千克)与销售价格x(元/千克)满足函数关系式![]() ,从市场反馈的信息发现,该海鲜食材每天的市场需求量q(千克)与销售价格x(元/千克)满足一次函数关系,部分数据如下表:
,从市场反馈的信息发现,该海鲜食材每天的市场需求量q(千克)与销售价格x(元/千克)满足一次函数关系,部分数据如下表:
销售价格x(元/千克) | 10 | 12 | … | 30 |
市场需求量q(千克) | 30 | 28 | … | 10 |
(已知按物价部门规定销售价格x不低于10元/千克且不高于30元/千克)
(1)请写出q与x的函数关系式:___________________________;
(2)当每天的进货量小于或等于市场需求量时,这种海鲜食材能全部售出,而当每天的进货量大于市场需求量时,只能售出符合市场需求量的海鲜食材,剩余的海鲜食材由于保质期短而只能废弃.
①求出每天获得的利润y(元)与销售价格x的函数关系式;
②为了避免浪费,每天要确保这种海鲜食材能全部售出,求销售价格为多少元时,每天获得的利润(元)最大值是多少?