题目内容
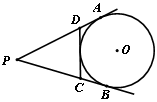
如图,在Rt△ABC中,∠C=90°,点D在AB上,以BD为直径的⊙O与AC交于点E,且BE平分∠ABC,

(1)判断直线AC与⊙O的位置关系,并说明理由;
(2)若AD=2,AE= ,求⊙O的面积.
,求⊙O的面积.

(1)判断直线AC与⊙O的位置关系,并说明理由;
(2)若AD=2,AE=
 ,求⊙O的面积.
,求⊙O的面积.(1)直线AC与⊙O相切,证明见解析;(2)⊙O的面积为: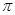 .
.
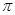 .
.试题分析:(1)取BD的中点O,连接OE,证明∠OEB=∠CBE后可得OE⊥AC;
(2)设⊙O的半径为r,则在Rt△AOE中,利用勾股定理列出有关半径的方程求得半径,即可求⊙O的面积.
试题解析:(1)直线AC与⊙O相切,理由是:
连接OE
∵OB=OE
∴∠OBE=∠OEB
∵∠OBE=∠CBE
∴∠OEB=∠CBE
∴OE ∥ BC
∴∠AEO=∠C=90°
∴ AC是⊙O的切线;
(2)设半径为r,根据勾股定理
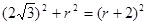
r=2
⊙O的面积为:
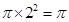 .
.
练习册系列答案
相关题目
 中,将一块含
中,将一块含 的直角三角板的
的直角三角板的 两点(点
两点(点 在
在 内部),
内部), 与
与 交于点
交于点 ,
, 交于点
交于点 .
.
 的度数;
的度数; 的中点,求
的中点,求 的值;
的值;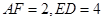 ,求
,求 的长.
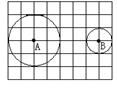
的长.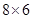 的网格图(每个小正方形的边长均为1个单位长度)中,⊙A的半径为2个单位长度,⊙B的半径为1个单位长度,要使运动的⊙B与静止的⊙A内切,应将⊙B由图示位置向左平移 个单位长度.
的网格图(每个小正方形的边长均为1个单位长度)中,⊙A的半径为2个单位长度,⊙B的半径为1个单位长度,要使运动的⊙B与静止的⊙A内切,应将⊙B由图示位置向左平移 个单位长度.