题目内容
如图,半圆 中,将一块含
中,将一块含 的直角三角板的
的直角三角板的 角顶点与圆心
角顶点与圆心 重合,角的两条边分别与半圆圆弧交于
重合,角的两条边分别与半圆圆弧交于 两点(点
两点(点 在
在 内部),
内部), 与
与 交于点
交于点 ,
, 与
与 交于点
交于点 .
.

(1)求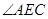 的度数;
的度数;
(2)若 是
是 的中点,求
的中点,求 的值;
的值;
(3)若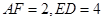 ,求
,求 的长.
的长.
 中,将一块含
中,将一块含 的直角三角板的
的直角三角板的 角顶点与圆心
角顶点与圆心 重合,角的两条边分别与半圆圆弧交于
重合,角的两条边分别与半圆圆弧交于 两点(点
两点(点 在
在 内部),
内部), 与
与 交于点
交于点 ,
, 与
与 交于点
交于点 .
.
(1)求
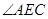 的度数;
的度数;(2)若
 是
是 的中点,求
的中点,求 的值;
的值;(3)若
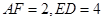 ,求
,求 的长.
的长.(1)证明见解析;(2)  ;
;
 ;
;试题分析:(1)连接AC,根据直径所对的圆周角为直角可知
 ,根据圆周角定理可知,同弧所对的圆周角等于圆心角的一半可得到
,根据圆周角定理可知,同弧所对的圆周角等于圆心角的一半可得到 ,在直角三角形再根据直角三角形内角和定理可知
,在直角三角形再根据直角三角形内角和定理可知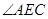 =
= ;(2)根据点C是弧AD的中点,及半径的性质,可以得到
;(2)根据点C是弧AD的中点,及半径的性质,可以得到 ,得到
,得到 角的性质可知
角的性质可知 ,所以的到比例线段;(3)结合前面两问的结论,可以首先证明两个三角形相似,然后结合直角三角形的勾股定理可以求得线段长.
,所以的到比例线段;(3)结合前面两问的结论,可以首先证明两个三角形相似,然后结合直角三角形的勾股定理可以求得线段长.试题解析:解 (1)如图,连接
 .
.
 是直径,
是直径,
 ,
,
 ,
,
 ,
,
 ,
,(2)

 是
是 的中点,
的中点, 是半径,
是半径,
 ,
,
 ,
,
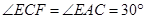 ,
,即
 ,
,

即
 (或
(或 ) ;
) ;(3) 连接
 ,过点
,过点 作
作 的垂线,垂足为
的垂线,垂足为 ,
,设
 ,
,则
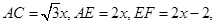
在
 中,
中, ,
,
 ,
,
 ,
, ,
,
 ∽
∽ ,
,
 ,
,即
 ,
,在
 中,由勾股定理,
中,由勾股定理, ,
,即
 ,
,即
 ,
,解得:
 (不合题意,舍去),
(不合题意,舍去), ,
,
 .
.

练习册系列答案
相关题目



 ,求⊙O的面积.
,求⊙O的面积.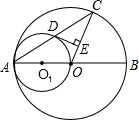

 是⊙O上的点,若
是⊙O上的点,若 ,则
,则 ___________度.
___________度.

