题目内容
如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上．已知纸板的两条直角边DF=50cm，EF=30cm，测得边DF离地面的高度AC=1.5m，CD=20m，则树高AB为（ ）
| A．12m | B．13.5m | C．15m | D．16.5m |
D．
解析试题分析：∵∠DEF=∠BCD=90°，∠D=∠D，∴△DEF∽△DCB. ∴
.
∵DF=50cm=0.5m，EF=30cm=0.3m，AC=1.5m，CD=20m，∴由勾股定理求得DE=0.40m.
∴
，解得BC="15" m. ∴AB="AC+BC=1.5+15=16.5" m.
故选D．
考点：1相似三角形的应用；2.勾股定理．
练习册系列答案
阅读快车系列答案
相关题目
如图，△ABC中，AD⊥BC于D，且有下列条件：（1）∠B＋∠DAC＝90°；（2）∠B＝∠DAC；（3）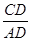
＝
；（4）AB2＝BD·BC其中一定能够判定△ABC是直角三角形的共有（ ）
| A．3个 | B．2个 | C．1个 | D．0个 |
下列四组图形中，一定相似的是
| A．矩形与矩形 | B．正方形与菱形 | C．菱形与菱形 | D．正方形与正方形 |
如图，在Rt△ABC中，∠C=90°，P是斜边上一定点，过点P作直线与一直角边交于点Q使图中出现两个相似三角形，这样的点Q有 ( )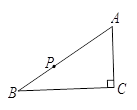
| A．1个 | B．2个 | C．3个 | D．4个 |
如图，直线
与x轴， y轴分别相交于A，B两点，C为OB上一点，且
，则S△ABC等于 ( )
| A．1 | B．2 | C．3 | D．4 |
（顶点均在格点上），若它们是以点P为位似中心的位似图形，则点P的坐标是（ ）
如图，在△ABC中，AB＝AC，∠A＝36°，BD平分∠ABC交AC于点D，若AC＝2，则AD的长是( )
A． | B． |
C． －1 | D．＋1 |
