题目内容
如图,直线 与x轴, y轴分别相交于A,B两点,C为OB上一点,且
与x轴, y轴分别相交于A,B两点,C为OB上一点,且 ,则S△ABC等于 ( )
,则S△ABC等于 ( )
| A.1 | B.2 | C.3 | D.4 |
C.
解析试题分析:先根据直线的方程求出A、B两点的坐标,再根据角相等可得出三角形相似,最后通过相似比即可得出S△ABC的大小:
∵直线 与x轴,y轴分别相交于A,B两点,∴OA=2,OB=4.
与x轴,y轴分别相交于A,B两点,∴OA=2,OB=4.
又∵∠1=∠2,∴∠BAO=∠OCA. ∴△OAC∽△OAB.
∴OC:OA=OA:OB=1:2. ∴OC=1,BC=3.
∴S△ABC= ×2×3=3.
×2×3=3.
故选C.
考点:1.坐标与图形性质;2.一次函数图象上点的坐标特征;3.相似三角形的判定和性质.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DF=50cm,EF=30cm,测得边DF离地面的高度AC=1.5m,CD=20m,则树高AB为( )
| A.12m | B.13.5m | C.15m | D.16.5m |
如图,矩形AEHC是由三个全等矩形拼成的,AH与BE、BF、DF、DG、CG分别交于点P、Q、K、M、N,设△BPQ, △DKM, △CNH 的面积依次为S1,S2,S3。若S1+ S3=20,则S2的值为 ( ) 
| A.8 | B.10 | C.12 | D. |
如图所示,△ABC∽△DEF 其相似比为K , 则一次函数 的图像与两坐标轴围成的三角形面积是( )
的图像与两坐标轴围成的三角形面积是( )
| A.0.5 | B.4 | C.2 | D. 1 |
在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为2,把△EFO放大,则点E的对应点E′的坐标是( )
| A.(-2,1) | B.(-8,4) |
| C.(-8,4)或(8,-4) | D.(-2,1)或(2,-1) |
已知△ABC∽△DEF,且AB:DE=1:2,则△ABC的周长与△DEF的周长之比为 ( )
| A.2:1 | B.1:2 | C.1:4 | D.4:1 |
下列四个命题中,属于真命题的是
A.若 ,则a=m ,则a=m |
| B.若a>b,则am>bm |
| C.两个等腰三角形必定相似 |
| D.位似图形一定是相似图形 |
 ,
, ,延长
,延长 交
交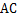 于
于 ,且
,且 ,则
,则
 B.
B.
 D.
D.