题目内容
【题目】甲船从![]() 码头出发顺流驶向
码头出发顺流驶向![]() 码头,同时乙船从
码头,同时乙船从![]() 码头出发逆流驶向
码头出发逆流驶向![]() 码头,甲,乙两船到达
码头,甲,乙两船到达![]() ,
,![]() 两码头后立即返回,乙船返回后行驶20千米与返回的甲船相遇,甲,乙两船在静水中的平均速度不变,
两码头后立即返回,乙船返回后行驶20千米与返回的甲船相遇,甲,乙两船在静水中的平均速度不变,![]() ,
,![]() 两码头间的水流速度为4千米/时,甲船逆流而行的速度与乙船顺流而行的速度相等,甲船顺流而行速度是乙船逆流而行速度的2倍,则
两码头间的水流速度为4千米/时,甲船逆流而行的速度与乙船顺流而行的速度相等,甲船顺流而行速度是乙船逆流而行速度的2倍,则![]() ,
,![]() 两码头间的路程为_______千米.
两码头间的路程为_______千米.
【答案】160
【解析】
由题意先设乙船逆流而行的速度为m千米/时,并建立方程求出m的值,再设![]() ,
,![]() 两码头间的路程为x千米,建立方程求解即可.
两码头间的路程为x千米,建立方程求解即可.
解:设乙船逆流而行的速度为m千米/时,甲船顺流而行的速度为2m千米/时,根据甲船逆流而行的速度与乙船顺流而行的速度相等可得:
![]() ,解得
,解得![]() ,
,
即有乙船逆流而行的速度为16千米/时,乙船顺流而行的速度为24千米/时,
甲船逆流而行的速度为24千米/时,甲船顺流而行的速度为32千米/时,
又设![]() ,
,![]() 两码头间的路程为x千米,根据题意建立方程:
两码头间的路程为x千米,根据题意建立方程:
![]() ,解得
,解得![]() ,
,
所以![]() ,
,![]() 两码头间的路程为160千米.
两码头间的路程为160千米.
故答案为:160.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
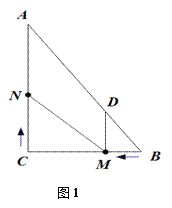
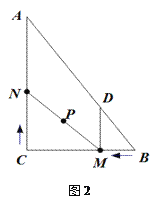
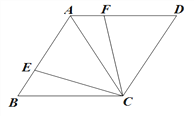
【题目】如图,四边形ABCD中,∠B=60°,对角线AC=BC,点E在AB上,将CE绕点C顺时针旋转60得CF,且点F在AD上.
(1)求证:AF=BE;
(2)若AE=DF,求证:四边形ABCD是菱形.
【题目】简单多面体是各个面都是多边形组成的几何体,十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)和棱数(E)之间存在一个有趣的关系式,称为欧拉公式.如表是根据左边的多面体模型列出的不完整的表:
多面体 | 顶点数 | 面数 | 棱数 |
四面体 | 4 | 4 | 6 |
长方体 | 8 | 6 | |
正八面体 | 8 | 12 |
现在有一个多面体,它的每一个面都是三角形,它的面数(F)和棱数(E)的和为30,则这个多面体的顶点数V=_____.