��Ŀ����
����Ŀ��ij�̳����ۼס�������Ʒ�Ƶ������ֻ����������ֻ��Ľ��ۺ��ۼ����±���ʾ��
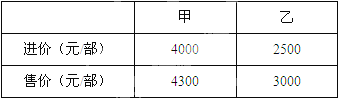
���̳��ƻ����������ֻ����ɲ�������15��5��Ԫ��Ԥ��ȫ�����ۺ�ɻ�ë����2��1��Ԫ��
��ë����=���ۼ۩����ۣ�����������
��1�����̳��ƻ������ס��������ֻ������ٲ���
��2�� ͨ���г����У����̳�������ԭ�ƻ��Ļ����ϣ����ټ����ֻ��Ĺ������������������ֻ��Ĺ�����������֪�����ֻ����ӵ������Ǽ����ֻ����ٵ�������2�����������ڹ����������ֻ������ʽ���16��Ԫ�����̳�����������ʹȫ�����ۺ��õ�ë�������������ë������
���𰸡���1�������ֻ���20���������ֻ���30������2���������Ϊ24500Ԫ��
��������
�����������1��������ֻ�����x�����������ֻ�������155000-4000x����2500����������������2��Ԫ��������ʽ�����⼴�ɣ�
��2��������ֻ�����m����ë����ΪyԪ�������m��ȡֵ��Χ����������=�ۼ�-���۽�����������ʽ������
�����������1��������ֻ�����x���������⣬��
300x+500��![]() ��20000��
��20000��
�����x��22��
�������ֻ�������Ϊ������
��x�����ֵΪ20��
�������ֻ�Ӧ�ù�����155000-4000��20����2500=30����
��Ҫ�뾡���ܶ�Ĺ��������ֻ���Ӧ�ð��������Ľ����������������ֻ���20���������ֻ���30����
��2��������ֻ�����m����ë����ΪyԪ�������⣬��
4000��20-m��+2500��30+2m����160000��
�����m��5��
y=300��20-m��+500��30+2m����
y=700m+21000��
��k=700��0��
��y��m�����������
��m=5ʱ���������Ϊ24500Ԫ��

 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�����Ŀ�����꼶һ��Ͷ������ѡ![]() ��ͬѧ����Ͷ�����������ձ�������ÿ�˸�Ͷ��
��ͬѧ����Ͷ�����������ձ�������ÿ�˸�Ͷ��![]() ����������ѡ�ֵĽ�����ͳ�����±�������ݱ������ݻش����⣮
����������ѡ�ֵĽ�����ͳ�����±�������ݱ������ݻش����⣮
������������ |
|
|
|
|
|
|
һ���������ˣ� |
|
|
|
|
|
|
�����������ˣ� |
|
|
|
|
|
|
![]() �����
�����
ƽ���� | ��λ�� | ���� | ���� | |
һ�� | 2.6 | |||
���� | 7 | 7 | 7 |
![]() ���Ҫ������������ѡ��һ������������μ�ѧУ��Ͷ����������ȡ����ܽ����������һ��������ΪӦ��ѡ���ĸ��ࣿ���Ҫ��ȡ���˽���������ѧУǰ����������ΪӦ��ѡ���ĸ��ࣿ
���Ҫ������������ѡ��һ������������μ�ѧУ��Ͷ����������ȡ����ܽ����������һ��������ΪӦ��ѡ���ĸ��ࣿ���Ҫ��ȡ���˽���������ѧУǰ����������ΪӦ��ѡ���ĸ��ࣿ