��Ŀ����
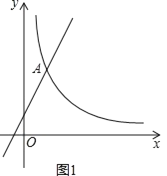
����Ŀ����ͼ����֪��A��ֱ��y=2x+1�뷴��������![]() (x��0)ͼ��Ľ��㣬�ҵ�A�ĺ�����Ϊ1��
(x��0)ͼ��Ľ��㣬�ҵ�A�ĺ�����Ϊ1��
(1)��k��ֵ��
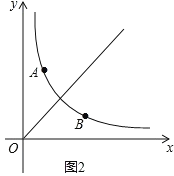
(2)��ͼ1��˫����![]() (x��0)��һ��M����S��AOM=4�����M�����ꣻ
(x��0)��һ��M����S��AOM=4�����M�����ꣻ
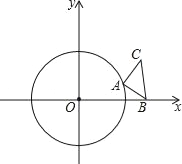
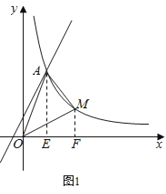
(3)��ͼ2��ʾ������֪����������![]() (x��0)ͼ����һ��B(3��1)����P��ֱ��y=x��һ���㣬��Q�Ƿ���������
(x��0)ͼ����һ��B(3��1)����P��ֱ��y=x��һ���㣬��Q�Ƿ���������![]() (x��0)ͼ������һ�㣬�Ƿ������P��A�� B��QΪ�����ƽ���ı���?�����ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�
(x��0)ͼ������һ�㣬�Ƿ������P��A�� B��QΪ�����ƽ���ı���?�����ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��k��3��2��M��3��1����M��![]() ��9����3��Q1��
��9����3��Q1��![]() ��2��
��2��![]() 2����Q2��
2����Q2��![]() 2��
2��![]() ��2����Q3��
��2����Q3��![]() ��
��![]() ����
����
��������
��1����A��ֱ��y��2x��1�ĵ㣬��A�ĺ�����Ϊ1������y��2��1��1��3����õ�A���ɵõ������
��2����ͼ1�����M��m��![]() ������A��AE��x����E����M��MF��x����F����������ã�S��AOM��S����AEFM�ⷽ�̼��ɵõ������
������A��AE��x����E����M��MF��x����F����������ã�S��AOM��S����AEFM�ⷽ�̼��ɵõ������
��3��������÷����������Ľ���ʽ��Ȼ����P��m��m��������PQΪƽ���ı��εıߺ���PQΪƽ���ı��εĶԽ�����������������ۼ���ȷ����Q�����꣮
��1���ߵ�A��ֱ��y��2x��1�ĵ㣬��A�ĺ�����Ϊ1��
��y��2��1��1��3��
��A��1��3����
�ߵ�A�Ƿ���������y��![]() ��x��0��ͼ���ϵĵ㣬
��x��0��ͼ���ϵĵ㣬
��k��3��
��2����ͼ1�����M��m��![]() ������A��AE��x����E����M��MF��x����F��
������A��AE��x����E����M��MF��x����F��
��M��A���Ҳ�ʱ����������ã�S��AOM��S����AEFM��![]() ��3��
��3��![]() ������m1����4��
������m1����4��
��ã�m��3��m=-![]() ����ֵ��ȥ����
����ֵ��ȥ����
��M��A���Ҳ�ʱ����������ã�S��AOM��S����AEFM��![]() ��3��
��3��![]() ������1m����4��
������1m����4��
��ã�m��![]() ��m=-3����ֵ��ȥ����
��m=-3����ֵ��ȥ����
���ϣ�m��3��![]() ��
��
��M��3��1����M��![]() ��9����
��9����
��3���߷���������y��![]() ��x��0��ͼ����A��1��3����
��x��0��ͼ����A��1��3����
��k��1��3��3��
�෴���������Ľ���ʽΪy��![]() ��
��
�ߵ�P��ֱ��y��x�ϣ�
����P��m��m��
����PQΪƽ���ı��εıߣ�
�ߵ�A�ĺ�����ȵ�B�ĺ�����С2����A��������ȵ�B���������2��
���Q�ڵ�P���·������Q������Ϊ��m��2��m2����ͼ2��
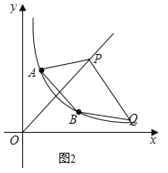
����Q�ڵ�P���Ϸ������Q������Ϊ��m2��m��2����ͼ3��
��Q��m��2��m2�����뷴���������Ľ���ʽ�ã���m��2����m-2��=3
m����![]() ��
��
��m��0��
��m��![]() ��
��
��Q1��![]() ��2��
��2��![]() 2����
2����
ͬ���ɵ���һ��Q2��![]() 2��
2��![]() ��2����
��2����
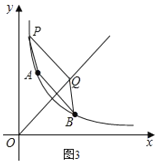
����PQΪƽ���ı��εĶԽ��ߣ���ͼ4��

��A��B����y��x�Գƣ�
��OP��AB
��ʱ��Q��ֱ��y��x�ϣ���Ϊֱ��y��x��˫����y��![]() �Ľ��㣬
�Ľ��㣬
��![]() ���
���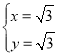 ��
��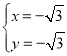 ����ȥ��
����ȥ��
��Q3��![]() ��
��![]() ��
��
�������������������ĵ�Q������������ֱ�Ϊ��Q1��![]() ��2��
��2��![]() 2����Q2��
2����Q2��![]() 2��
2��![]() ��2����Q3��
��2����Q3��![]() ��
��![]() ����
����

 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�