题目内容
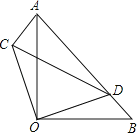
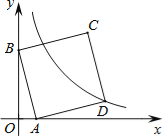
【题目】如图,正方形AOBC的边OB、OA分别在x、y轴上,点C坐标为(8,8),将正方形AOBC绕点A逆时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段BC于点Q,ED的延长线交线段OB于点P,连接AP、AQ.
(1)求证:△ACQ≌△ADQ;
(2)求∠PAQ的度数,并判断线段OP、PQ、CQ之间的数量关系,并说明理由;
(3)连接BE、EC、CD、DB得到四边形BECD,在旋转过程中,四边形BECD能否是矩形?如果能,请求出点P的坐标,如果不能,请说明理由.

【答案】(1)见解析,(2)PQ=OP+CQ,理由见解析,(3)![]() );理由见解析.
);理由见解析.
【解析】
(1)由正方形的性质及旋转的性质可得到AD=AC,利用HL即可证得结论;
(2)利用(1)的结论,结合条件可证得△AOP≌△ADP,进一步可求得∠PAQ=45°,再结合全等可求得PQ=OP+CQ;
(3)利用矩形的性质可得到BQ=EQ=CQ=DQ,设P(x,0),则可表示出BQ、PB的长,在Rt△BPQ中,利用勾股定理可得到关于x的方程,则可求得P点坐标.
(1)证明:
∵正方形AOBC绕点A旋转得到正方形ADEF,
∴AD=AC,∠ADQ=∠ACQ=90°,
在Rt△ADQ和Rt△ACQ中
![]() ,
,
∴Rt△ACQ≌Rt△ADQ(HL);
(2)解:
∵△ACQ≌△ADQ,
∴∠CAQ=∠DAQ,CQ=DQ,
在Rt△AOP和Rt△ADP中
![]() ,
,
∴Rt△AOP≌Rt△ADP(HL),
∴∠OAP=∠DAP,OP=OD,
∴∠PAQ=∠DAQ+DAP=![]() ∠DAC+
∠DAC+![]() ∠DAO=
∠DAO=![]() (∠DAC+∠DAO)=
(∠DAC+∠DAO)=![]() ∠OAC=45°,
∠OAC=45°,
PQ=PD+DQ=OP+CQ;
(3)解:四边形BECD可为矩形,如图,

若四边形BECD为矩形,则BQ=EQ=CQ=DQ,
∵BC=8,
∴BQ=CQ=4,
设P点坐标为(x,0),则PO=x,
∵OP=PD,CQ=DQ,
∴PD=x,DQ=4,
在Rt△BPQ中,可知PQ=x+4,BQ=4,BP=8﹣x,
∴(x+4)2+42=(8﹣x)2,解得x=![]() ,
,
∴P点坐标为(![]() ,0).
,0).

 智能训练练测考系列答案
智能训练练测考系列答案