题目内容
【题目】如图,△ABC是直角三角形,∠BAC=90°,D是斜边BC的中点,E,F分别是AB,AC边上的点,且DE⊥DF.
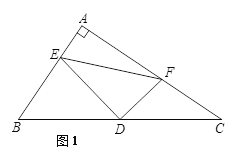

(1)如图1,试说明![]() ;
;
(2)如图2,若AB=AC,BE=12,CF=5,求△DEF的面积.
【答案】(1)、略 (2)、![]()
【解析】
(1)延长ED至G,使得DG=DE,根据△CDG≌△BDE,得到CG=BE;
(2)根据∠FCG=90°得到CG+CF=FG,根据中垂线的性质得到FG=EF,从而得到所求的结论.
(1)证明:延长ED至点G,使得DG=DE,连接FG,CG,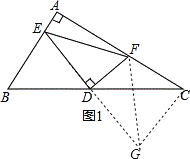
∵DE=DG,DF⊥DE,
∴DF垂直平分DE,
∴EF=FG,
∵D是BC中点,
∴BD=CD,
在△BDE和△CDG中,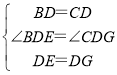 ,
,
∴△BDE≌△CDG(SAS),
∴BE=CG,∠DCG=∠DBE,
∵∠ACB+∠DBE=90°,
∴∠ACB+∠DCG=90°,即∠FCG=90°,
∵CG2+CF2=FG2,
∴BE2+CF2=EF2;
(2)解:连接AD,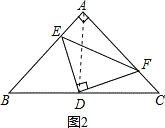
∵AB=AC,D是BC中点,
∴∠BAD=∠C=45°,AD=BD=CD,
∵∠ADE+∠ADF=90°,∠ADF+∠CDF=90°,
∴∠ADE=∠CDF,
在△ADE和△CDF中,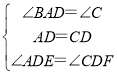 ,
,
∴△ADE≌△CDF(ASA),
∴AE=CF,BE=AF,AB=AC=17,
∴S四边形AEDF=![]() S△ABC,
S△ABC,

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目