题目内容
已知:关于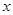 的一元二次方程
的一元二次方程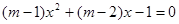 (m为实数)
(m为实数)
小题1:若方程有两个不相等的实数根,求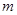 的取值范围;
的取值范围;
小题2:在(1)的条件下,求证:无论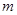 取何值,抛物线
取何值,抛物线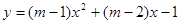 总过
总过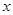 轴上的一个固定点;
轴上的一个固定点;
小题3:若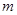 是整数,且关于
是整数,且关于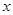 的一元二次方程
的一元二次方程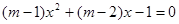 有两个不相等的整数根,把抛物线
有两个不相等的整数根,把抛物线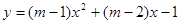 向右平移3个单位长度,求平移后的解析式.
向右平移3个单位长度,求平移后的解析式.
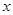 的一元二次方程
的一元二次方程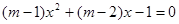 (m为实数)
(m为实数)小题1:若方程有两个不相等的实数根,求
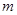 的取值范围;
的取值范围;小题2:在(1)的条件下,求证:无论
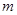 取何值,抛物线
取何值,抛物线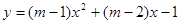 总过
总过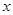 轴上的一个固定点;
轴上的一个固定点;小题3:若
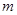 是整数,且关于
是整数,且关于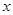 的一元二次方程
的一元二次方程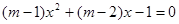 有两个不相等的整数根,把抛物线
有两个不相等的整数根,把抛物线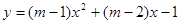 向右平移3个单位长度,求平移后的解析式.
向右平移3个单位长度,求平移后的解析式.小题1:(1)△=
 ∵方程有两个不相等的实数根,
∵方程有两个不相等的实数根,∴
 .∵
.∵ ,∴m的取值范围是
,∴m的取值范围是
小题2:证明:令
 得,
得, .
.∴
 .[ ∴
.[ ∴ ,
, .∴抛物线与x轴的交点坐标为(
.∴抛物线与x轴的交点坐标为( ),(
),( ),
),∴无论m取何值,抛物线
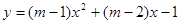 总过定点(
总过定点( )
)小题3:∵
 是整数 ∴只需
是整数 ∴只需 是整数.∵
是整数.∵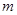 是整数,且
是整数,且 ,
,∴
 .当
.当 时,抛物线为
时,抛物线为 .
.把它的图象向右平移3个单位长度,得到的抛物线解析式为
 .
.略

练习册系列答案
相关题目

 与,2011年11月1日,“北京精神”表述语“爱国、创新、包容、厚德”正式向社会发布. 为了更好地宣传“北京精神”,小明同学参加了由街道组织的百姓宣讲小分队,利用周末时间到周边社区发放宣传材料. 第一周发放宣传材料300份,第三周发放宣传材料363份. 求发放宣传材料份数的周平均增长率.
与,2011年11月1日,“北京精神”表述语“爱国、创新、包容、厚德”正式向社会发布. 为了更好地宣传“北京精神”,小明同学参加了由街道组织的百姓宣讲小分队,利用周末时间到周边社区发放宣传材料. 第一周发放宣传材料300份,第三周发放宣传材料363份. 求发放宣传材料份数的周平均增长率.
 ,经过2010年第1季度和第2季度的涨价,商品房均价达3600元/
,经过2010年第1季度和第2季度的涨价,商品房均价达3600元/ .
. 
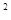 +x+a
+x+a