Question

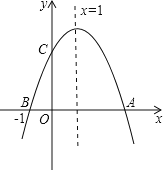
【题目】如图，在平面直角坐标系中，抛物线经过点，交轴于点.

（1）求抛物线的解析式.

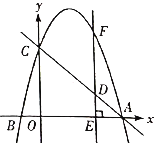
（2）点是线段上一动点，过点作垂直于轴于点，交抛物线于点，求线段的长度最大值.

Answer 1

【答案】（1）；（2）4.

【解析】

（1）根据A、B坐标可得抛物线两点式解析式，化为一般形式即可；

（2）根据抛物线解析式可得C点坐标，利用待定系数法可得直线AC的解析式为y=-x+4，设点坐标为，则，用m表示出DF的长，配方为二次函数顶点式的形式，根据二次函数的性质求出DF的最大值即可.

（1）∵拋物线经过点，

∴

∴拋物线的解析式为.

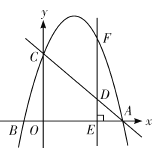
（2）∵拋物线的解析式为，

∴，

设直线的解析式为y=kx+b，

∴，

∴，b=4，

∴直线AC的解析式为

设点坐标为，则

∴=-(m-2)2+4，

∴当m=2时，DF的最大值为4.