题目内容
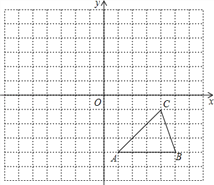
【题目】如图,在平行四边形ABCD中,连接AC,∠BAC=90°,AB=AC,点E是边BC上一点,连接DE,交AC于点F,∠ADE=30°.
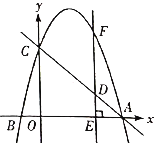
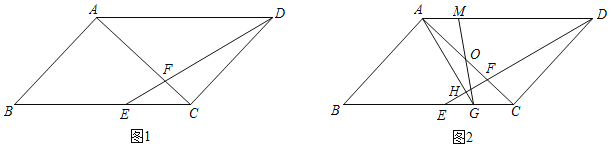
(1)如图1,若AF=2,求BC的长;
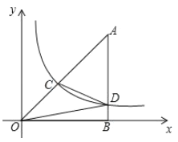
(2)如图2,过点A作AG⊥DE于点H,交BC于点G,点O是AC中点,连接GO并延长交AD于点M.求证:AG+CG=DM.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
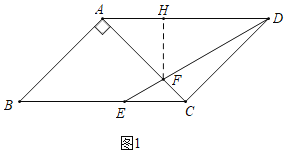
(1)如图1中,作FH⊥AD于H.解直角三角形求出AH,HD即可解决问题.
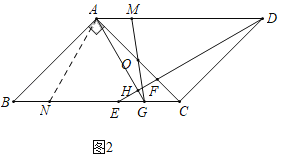
(2)如图2中,在BC上取一点N,使得∠BAN=∠CAG.利用全等三角形的性质证明DM=BG,再证明△ANG是等边三角形即可解决问题.
(1)解:如图1中,作FH⊥AD于H.
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠ACB=45°,
∵AF=2,
∴AH=HF=![]()
∵∠FDH=30°,
∴DH=![]() FH=
FH=![]() ,
,
∴BC=AD=![]()
![]()
(2)证明:如图2中,在BC上取一点N,使得∠BAN=∠CAG.
∵AM∥CG,
∴∠MAO=∠GCO,
∵AO=OC,∠AOM,∠COG,
∴△AOM≌△COG(ASA),
∴AM=CG,
∵AD=BC,
∴DM=BG,
∵AG⊥DE,
∴∠AHD=90°,
∵∠ADE=30°,
∴∠DAH=60°,
∵∠DAC=45°,
∴∠CAG=∠BAN=15°,
∴∠NAG=60°,
∵AB=AC,∠BAN=∠CAG,∠B=∠ACG=45°,
∴△ABN≌△ACG(ASA),
∴AN=AG,CG=BN,
∴△ANG是等边三角形,
∴AG=GN,
∴AG+CG=GN+BN=BG=DM.

练习册系列答案
相关题目