题目内容
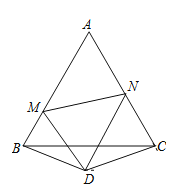
【题目】如图,在 ![]() 中,
中, ![]() ,
, ![]() ,将
,将 ![]() 绕点
绕点 ![]() 顺时针旋转
顺时针旋转 ![]() ,得到
,得到 ![]() ,连接
,连接 ![]() ,交
,交 ![]() 于点
于点 ![]() ,则
,则 ![]() 与
与 ![]() 的周长之和为
的周长之和为 ![]() .
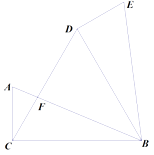
.
【答案】42
【解析】∵将△ABC绕点B顺时针旋转60°,得到△BDE,
∴△ABC≌△BDE,∠CBD=60°,
∴BD=BC=12cm,
∴△BCD为等边三角形,
∴CD=BC=CD=12cm,
在Rt△ACB中,AB= ![]() =
= ![]() =13,
=13,
△ACF与△BDF的周长之和=AC+AF+CF+BF+DF+BD=AC+AB+CD+BD=5+13+12+12=42(cm),
故答案为:42.
根据将△ABC绕点B顺时针旋转60°,得到△BDE,可得△ABC≌△BDE,∠CBD=60°,BD=BC=12cm,从而得到△BCD为等边三角形,得到CD=BC=CD=12cm,在Rt△ACB中,利用勾股定理得到AB=13,所以△ACF与△BDF的周长之和=AC+AF+CF+BF+DF+BD=AC+AB+CD+BD,即可解答.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
【题目】某校为了解九年级学生的视力情况,随机抽样调查了部分九年级学生的视力,以下是根据调查结果绘制的统计图表的一部分.
分组 | 视力 | 人数 |
A | 3.95≤x≤4.25 | 3 |
B | 4.25<x≤4.55 |
|
C | 4.55<x≤4.85 | 18 |
D | 4.85<x≤5.15 | 8 |
E | 5.15<x≤5.45 |
|
根据以上信息,解谷下列问题:
(1)在被调查学生中,视力在3.95≤x≤4.25范围内的人数为 人;
(2)本次调查的样本容量是 ,视力在5.15<x≤5.45范围内学生数占被调查学生数的百分比是 %;
(3)在统计图中,C组对应扇形的圆心角度数为 °;
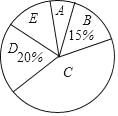
(4)若该校九年级有400名学生,估计视力超过4.85的学生数.