Question

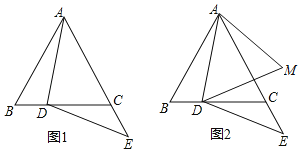
【题目】如图，在△ABC中，AD是高，AE是角平分线．

（1）若∠B=30°，∠C=70°，则∠CAE=______°，∠DAE=______°．

（2＞若∠B=40°，∠C=80°．则∠DAE=______°．

（3）通过探究，小明发现将（2）中的条件“∠B=40°，∠C=80°”改为“∠C-∠B=40°”，也求出了∠DAE的度数，请你写出小明的求解过程．

Answer 1

【答案】（1）40，20；（2） 20；（3）详见解析

【解析】

（1）根据三角形的高求出∠ADC=90°，再根据三角形内角和定理求出求出∠BAC和∠DAC，根据角平分线定义求出∠CAE，即可求出答案；

（2）根据三角形的高求出∠ADC=90°，再根据三角形内角和定理求出求出∠BAC和∠DAC，根据角平分线定义求出∠CAE，即可求出答案；

（3）根据三角形的高求出∠ADC=90°，再根据三角形内角和定理求出求出∠BAC和∠DAC，根据角平分线定义求出∠CAE，最后代入求出即可．

解：（1）∵∠B=30°，∠C=70°，

∴∠BAC=180°-（∠B+∠C）=80°，

∵AE是角平分线，

∴∠CAE= =40°，

∵AD是高，

∴∠ADC=90°，

∵∠C=70°，

∴∠DAC=180°-∠ADC-∠C=20°，

∴∠DAE=∠CAE-∠CAD=40°-20°=20°，

故答案为：40，20；

（2）∵∠B=40°，∠C=80°，

∴∠BAC=180°-（∠B+∠C）=60°，

∵AE是角平分线，

∴∠CAE==30°，

∵AD是高，

∴∠ADC=90°，

∵∠C=80°，

∴∠DAC=180°-∠ADC-∠C=10°，

∴∠DAE=∠CAE-∠CAD=30°-10°=20°，

故答案为：20；

（3）∵∠BAC +∠B+∠C=180°，

∴∠BAC=180°-（∠B+∠C），

∵AE是角平分线，

∴∠CAE=

∵AD是高，

∴∠ADC=90°，

∴∠DAC=180°-∠ADC-∠C=90°-∠C，

∴∠DAE=∠CAE-∠CAD

=20°．