题目内容
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B,分别向上平移2个单位,再向右平移1个单位,分别得到点A、B的对应点C、D,连接AC,BD,CD,得平行四边形ABDC.
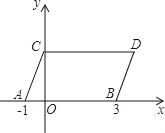
(1)直接写出点C,D的坐标;
(2)若在直线CD上存在点M,连接MA,MB,使S△MAB=2S△MBD,求出点M的坐标;
(3)若点P在直线BD上运动,连接PC,PO,请画出图形,写出∠CPO,∠DCP,∠BOP的数量关系,并说明理由.
【答案】(1)C(0,2),D(4,2);(2)M(2,2)或(6,2);(3)①当点P在BD上,∠CPO=∠DCP+∠BOP,见解析;②当点P在线段BD的延长线上时,∠CPO=∠BOP﹣∠DCP,见解析;③当点P在线段DB的延长线上时,∠CPO=∠DCP﹣∠BOP,见解析.
【解析】
(1)根据向上平移纵坐标加,向右平移横坐标加求出点C、D的坐标即可,
(2)先求出S△MAB=4,进而判断出SABCD=2S△MAB=2S△BCD,进而判断出S△MBD=2,再分两种情况即可得出结论;
(3)分三种情况,根据平移的性质可得AB∥CD,再过点P作PE∥AB,根据平行公理可得PE∥CD,然后根据两直线平行,内错角相等可得∠DCP=∠CPE,∠BOP=∠OPE即可得出结论.
解:(1)∵将A(﹣1,0),B(3,0)分别向上平移2个单位,再向右平移1个单位,
∴C(0,2),D(4,2);
(2)∵AB=4,CO=2,
∴S△MAB=![]() AB×OC=4,
AB×OC=4,
∵SABCD=AB×OC=8=2S△MAB=2S△BCD,
∵S△MAB=2S△MBD,
∴S△MBD=2,
当点M在边CD上时,
∴点M是CD的中点,
∴M(2,2),
当点M在CD的延长线上时,
利用对称性得,M'(6,2),
∴M(2,2)或(6,2);
(3)①当点P在BD上,如图1,
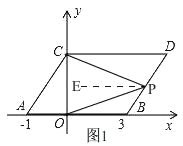
由平移的性质得,AB∥CD,
过点P作PE∥AB,则PE∥CD,
∴∠DCP=∠CPE,∠BOP=∠OPE,
∴∠CPO=∠CPE+∠OPE=∠DCP+∠BOP,
②当点P在线段BD的延长线上时,如图2,
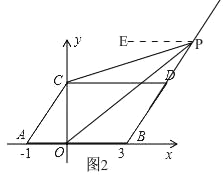
由平移的性质得,AB∥CD,
过点P作PE∥AB,则PE∥CD,
∴∠DCP=∠CPE,∠BOP=∠OPE,
∴∠CPO=∠OPE﹣∠CPE=∠BOP﹣∠DCP,
③当点P在线段DB的延长线上时,如图3,
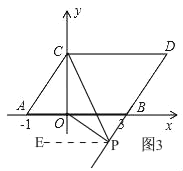
同(2)的方法得出∠CPO=∠DCP﹣∠BOP.