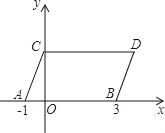
题目内容
【题目】完成下面的证明过程.
如图,已知,∠1+∠2=180°,∠A=∠D.求证AB∥CD.
证明:∵∠1+∠2=180°(已知)
∠1=∠3( )
∴∠3+∠2=180°( )
∴AE∥ ( )
∴∠D= ( )
∵∠A=∠D(已知)
∴∠A=∠CEA( )
∴AB∥CD ( )

【答案】对顶角相等,等量代换;DF;同旁内角互补,两直线平行,∠AEC;两直线平行,同位角相等,等量代换;内错角相等,两直线平行
【解析】
求出∠2+∠3=180°,根据平行线的判定得出AE∥DF,根据平行线的性质得出∠AEC=∠D,求出∠AEC=∠A,根据平行线的判定得出即可.
证明:∵∠1+∠2=180°(已知),
又∵∠1=∠3(对顶角相等),
∴∠2+∠3=180°(等量代换),
∴AE∥DF(同旁内角互补,两直线平行),
∴∠AEC=∠D(两直线平行,同位角相等),
∵∠A=∠D(已知)
∴∠AEC=∠A(等量代换)
∴AB∥CD(内错角相等,两直线平行),
故答案为:对顶角相等,等量代换;DF;同旁内角互补,两直线平行,∠AEC;两直线平行,同位角相等,等量代换;内错角相等,两直线平行.

【题目】根据绍兴市某风景区的旅游信息:
旅游人数 | 收费标准 |
不超过30人 | 人均收费80元 |
超过30人 | 每增加1人,人均收费降低1元,但人均收费不低于55元 |
A公司组织一批员工到该风景区旅游,支付给旅行社2800元.A公司参加这次旅游的员工有多少人?
【题目】在一个不透明的袋子中装有仅颜色不同的![]() 个小球,其中红球
个小球,其中红球![]() 个,白球
个,白球![]() 个.
个.
(1)先从袋子中取出![]() 个红球(
个红球(![]() 且
且![]() 为正整数),再从袋子中随机摸
为正整数),再从袋子中随机摸![]() 个小球,将“摸出白球”记为事件A,请完成下面表格:
个小球,将“摸出白球”记为事件A,请完成下面表格:
事件 | 必然事件 | 随机事件 |
|
(2)先从袋子中取出![]() 个红球,再放入
个红球,再放入![]() 个一样的白球并掘匀,随机摸出
个一样的白球并掘匀,随机摸出![]() 个白球的频率在
个白球的频率在![]() 附近摆动,求
附近摆动,求![]() 的值.
的值.