题目内容
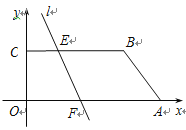
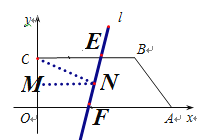
【题目】如图,在直角坐标系中,O(0,0),A(7,0),B(5,2),C(0,2)一条动直线l分别与BC、OA交于 点E、F,且将四边形OABC分为面积相等的两部分,则点C到动直线l的距离的最大值为____,
【答案】![]()
【解析】
设M、N分别是OC,EF的中点,若直线l将梯形OABC分为面积相等的两部分,则根据梯形的面积公式就可以求出CE+OF=6,由此可以得到MN=3,并且N是一个定点,若要C到l的距离最大,则l⊥CN,此时点C到动直线l的距离的最大值就是CN的长.
设M、N分别是OC,EF的中点.
∵O(0,0),A(7,0),B(5,2),C(0,2),
∴OA=7,OC=2,BC=5,
∴S梯形ABCD=![]() .
.
若直线l将梯形ABCD分为面积相等的两部分,则S梯形OCEF=![]() S梯形ABCD=6,
S梯形ABCD=6,
∴![]() ,
,
∴CE+OF=6,
∴MN=3,
∴N是一个定点
若要C到l的距离最大,则l⊥CN,
此时点A到动直线l的距离的最大值就是CN的长.
在Rt△CMN中,CM=1,MN=3
∴AN=![]() .
.
故答案为:![]() .
.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目