题目内容
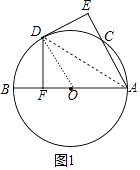
【题目】如图,AB为⊙O的直径,C为⊙O上一点,点D是弧BC的中点,DE⊥AC于点E,DE⊥AB于点F. 
(1)求证:DE是⊙O的切线;
(2)若OF=2,求AC的长度.
【答案】
(1)证明:连接OD、AD.
∵点D是 ![]() 的中点,
的中点,
∴ ![]() =
= ![]() ,
,
∴∠DAO=∠DAC,
∵OA=OD,
∴∠DAO=∠ODA,
∴∠DAC=∠ODA,
∴OD∥AE,
∵DE⊥AE,
∴∠AED=90°,
∴∠AED=∠ODE=90°,
∴OD⊥DE,
∴DE是⊙O的切线
(2)解:连接BC.
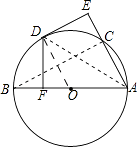
∵AB是⊙O直径,
∴∠ACB=90°,
∵OD∥AE,
∴∠DOB=∠EAB,
∵∠DFO=∠ACB=90°,
∴△DFO∽△BCA,
∴ ![]() =
= ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
∴AC=4
【解析】(1)连接OD、AD.只要证明OD∥AE,由DE⊥AC,推出DE⊥OD即可解决问题;(2)连接BC.只要证明△DFO∽△BCA,推出 ![]() =
= ![]() =
= ![]() 即可解决问题;
即可解决问题;
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对垂径定理的理解,了解垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.

【题目】随着科技的发展,电动汽车的性能得到显著提高,某市对市场上电动汽车的性能进行随机抽样调查,现随机抽取部分电动汽车,记录其一次充电后行驶的里程数,并将抽查数据绘制成如下频数分布直方表和条形统计图. 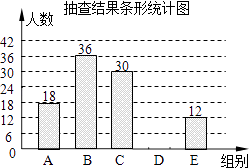
根据以上信息回答下列问题:
组别 | 行驶里程x(千米) | 频数(台) | 频率 |
A | x<200 | 18 | 0.15 |
B | 200≤x<210 | 36 | a |
C | 210≤x<220 | 30 | 0.25 |
D | 220≤x<230 | b | 0.20 |
E | x≥230 | 12 | 0.10 |
根据以上信息回答下列问题:
(1)填空:a= , b=;
(2)请将条形统计图补充完整;
(3)若该市市场上的电动汽车有2000台,请你估计电动汽车一次充电后行驶的里程数在220千米及以上的台数.