题目内容
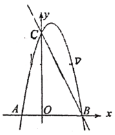
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(4,0),点C坐标为(0,4),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(4,0),点C坐标为(0,4),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
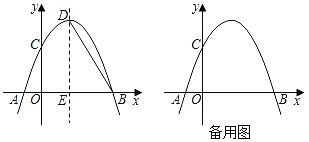
(1)求抛物线的解析式及点D的坐标;
(2)点F是抛物线上的动点,当∠FBA=2∠BDE时,求点F的坐标;
(3)若点P是x轴上方抛物线上的动点,以PB为边作正方形PBGH,随着点P的运动,正方形的大小、位置也随着改变,当顶点G或H恰好落在y轴上时,请直接写出点P的横坐标.
【答案】(1)y=﹣![]() x2+x+4;
x2+x+4;![]() ;(2)F(﹣
;(2)F(﹣![]() ,﹣
,﹣![]() )或(
)或(![]() ,
,![]() );(3)P的横坐标为
);(3)P的横坐标为![]() 或2或0或2﹣
或2或0或2﹣![]()
【解析】
(1)将点B、C的坐标代入抛物线表达式,即可求出解析式;将解析式化为顶点式即可得出点D的坐标;
(2)在线段DE上取点M,使MD=MB,此时∠EMB=2∠BDE,则∠FBA=∠EMB,即可求解;
(3)分点P在对称轴右侧、点P在对称轴左侧两种情况,利用三角形全等求解即可.
(1)将点B(4,0)、C(0,4)的坐标代入抛物线表达式得:
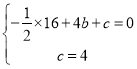 ,解得:
,解得:![]() ,
,
故抛物线的表达式为:y=-![]() x2+x+4=-
x2+x+4=-![]() (x﹣1)2+
(x﹣1)2+![]() ;
;
![]() 点D的坐标为
点D的坐标为![]()
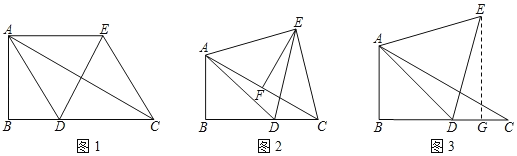
(2)如图1,在线段DE上取点M,使MD=MB,此时∠EMB=2∠BDE,
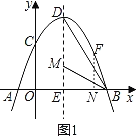
设ME=a,
由(1)得顶点D的坐标为(1,![]() ),
),
∵点B、C的坐标分别为(4,0)、(0,4),
∴BE= BO-EO=4-1=![]() ,
,
∴BM=MD=DE-ME=![]() ,
,
在Rt△BME中,ME2+BE2=BM2,即a2+32=(![]() ﹣a)2,解得:a=
﹣a)2,解得:a=![]() ,
,
∴tan∠EMB= =
=![]() ,
,
过点F作FN⊥x轴于点N,设点F(m,﹣![]() m2+m+4),则FN=|﹣
m2+m+4),则FN=|﹣![]() m2+m+4|,
m2+m+4|,
∵∠FBA=2∠BDE,
∴∠FBA=∠EMB,
∴tan∠FBA=tan∠EMB=![]() ,
,
∵点B(4,0)、点E(1,0),
∴BE=3,BN=4﹣m,
∴tan∠FBA=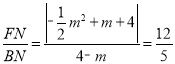 ,
,
解得:m=4(舍去)或﹣![]() 或
或![]() ,
,
故点F(﹣![]() ,﹣
,﹣![]() )或(
)或(![]() ,
,![]() );
);
(3)①当点P在对称轴右侧时,
(Ⅰ)当点H在y轴上时,如图2,
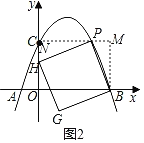
∵∠MPB+∠CPH=90°,∠CPH+∠CHP=90°,
∴∠CHP=∠MPB,
∵∠BMP=∠PNH=90°,PH=BP,
∴△BMP≌△PNH(AAS),
∴MB=PC,
设点P(x,y),则x=y=﹣![]() x2+x+4,
x2+x+4,
解得:x=![]() 或x=
或x=![]() (舍去负值),
(舍去负值),
故点P的横坐标为![]() ;
;
(Ⅱ)当点G在y轴上时,如图3,
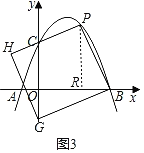
过点P作PR⊥x轴于点R,
同理可得:△PRB≌△BOG(AAS),
∴PR=OB=4,
即yP=4=﹣![]() x2+x+4,
x2+x+4,
解得:x=2;
②当点P在对称轴左侧时,
同理可得:点P的横坐标为0或2﹣![]() ;
;
综上,点P的横坐标为![]() 或2或0或2﹣
或2或0或2﹣![]() .
.

【题目】为迎接2022年冬奥会,鼓励更多的大学生参与到志愿服务中,甲、乙两所学校组织了志愿服务团队选拔活动,经过初选,两所学校各有300名学生进入综合素质展示环节,为了了解这些学生的整体情况,从两校进入综合素质展示环节的学生中分别随机抽取了50名学生的综合素质展示成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
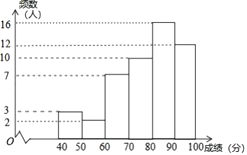
a.甲学校学生成绩的频数分布直方图如图(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
b.甲学校学生成绩在![]() 这一组是:
这一组是:
80 80 81 81.5 82 83 83 84
85 86 86.5 87 88 88.5 89 89
c.乙学校学生成绩的平均数、中位数、众数、优秀率(85分及以上为优秀)如下:
平均数 | 中位数 | 众数 | 优秀率 |
83.3 | 84 | 78 | 46% |
根据以上信息,回答下列问题:
(1)甲学校学生![]() ,乙学校学生
,乙学校学生![]() 的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“
的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“![]() ”或“
”或“![]() ”);
”);
(2)根据上述信息,推断________学校综合素质展示的水平更高,理由为:__________________________
(至少从两个不同的角度说明推断的合理性).
(3)若每所学校综合素质展示的前120名学生将被选入志愿服务团队,预估甲学校分数至少达到________分的学生才可以入选.