题目内容
【题目】若平面直角坐标系内的点M满足横、纵坐标都为整数,则把点M叫做“整点”.例如:P(1,0)、Q(2,﹣2)都是“整点”.抛物线y=mx2﹣4mx+4m﹣2(m>0)与x轴交于点A、B两点,若该抛物线在A、B之间的部分与线段AB所围成的区域(包括边界)恰有七个整点,则m的取值范围是( )
A. ![]() ≤m<1B.
≤m<1B. ![]() <m≤1C. 1<m≤2D. 1<m<2
<m≤1C. 1<m≤2D. 1<m<2
【答案】B
【解析】
画出图象,利用图象可得m的取值范围
∵y=mx2﹣4mx+4m﹣2=m(x﹣2)2﹣2且m>0,
∴该抛物线开口向上,顶点坐标为(2,﹣2),对称轴是直线x=2.
由此可知点(2,0)、点(2,﹣1)、顶点(2,﹣2)符合题意.
①当该抛物线经过点(1,﹣1)和(3,﹣1)时(如答案图1),这两个点符合题意.
将(1,﹣1)代入y=mx2﹣4mx+4m﹣2得到﹣1=m﹣4m+4m﹣2.解得m=1.
此时抛物线解析式为y=x2﹣4x+2.
由y=0得x2﹣4x+2=0.解得![]()
∴x轴上的点(1,0)、(2,0)、(3,0)符合题意.
则当m=1时,恰好有 (1,0)、(2,0)、(3,0)、(1,﹣1)、(3,﹣1)、(2,﹣1)、(2,﹣2)这7个整点符合题意.
∴m≤1.【注:m的值越大,抛物线的开口越小,m的值越小,抛物线的开口越大】
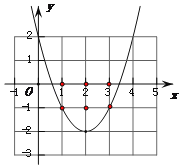
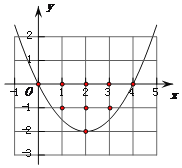
答案图1(m=1时) 答案图2( m=![]() 时)
时)
②当该抛物线经过点(0,0)和点(4,0)时(如答案图2),这两个点符合题意.
此时x轴上的点 (1,0)、(2,0)、(3,0)也符合题意.
将(0,0)代入y=mx2﹣4mx+4m﹣2得到0=0﹣4m+0﹣2.解得m=![]() .
.
此时抛物线解析式为y=![]() x2﹣2x.
x2﹣2x.
当x=1时,得![]() .∴点(1,﹣1)符合题意.
.∴点(1,﹣1)符合题意.
当x=3时,得![]() .∴点(3,﹣1)符合题意.
.∴点(3,﹣1)符合题意.
综上可知:当m=![]() 时,点(0,0)、(1,0)、(2,0)、(3,0)、(4,0)、(1,﹣1)、(3,﹣1)、(2,﹣2)、(2,﹣1)都符合题意,共有9个整点符合题意,
时,点(0,0)、(1,0)、(2,0)、(3,0)、(4,0)、(1,﹣1)、(3,﹣1)、(2,﹣2)、(2,﹣1)都符合题意,共有9个整点符合题意,
∴m=![]() 不符合题.
不符合题.
∴m>![]() .
.
综合①②可得:当![]() <m≤1时,该函数的图象与x轴所围成的区域(含边界)内有七个整点,
<m≤1时,该函数的图象与x轴所围成的区域(含边界)内有七个整点,
故选:B.

 名校课堂系列答案
名校课堂系列答案【题目】绿色无公害蔬菜基地有甲、乙两种植户,他们种植了![]() 两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
种植户 | 种植 | 种植 | 总收入(单位:元) |
甲 |
|
|
|
乙 |
|
|
|
说明:不同种植户种植的同类蔬菜每亩的平均收入相等;亩为土地面积单位
![]() 求
求![]() 两类蔬菜每亩的平均收入各是多少元?
两类蔬菜每亩的平均收入各是多少元?
![]() 某种植户准备租
某种植户准备租![]() 亩地用来种植
亩地用来种植![]() 两类蔬菜,为了使总收入不低于
两类蔬菜,为了使总收入不低于![]() 元且种植
元且种植![]() 类蔬菜的面积多于种植
类蔬菜的面积多于种植![]() 类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案;
类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案;
![]() 在
在![]() 的基础上,指出哪种方案使总收入最大,并求出最大值.
的基础上,指出哪种方案使总收入最大,并求出最大值.
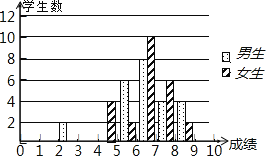
【题目】为了迎接体育中考,初三7班的体育老师对全班48名学生进行了一次体能模拟测试,得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格,成绩达到9分以上(包括9分)为优秀,这次模拟测试中男、女生全部成绩分布的条形统计图如下
(1)请补充完成下面的成绩统计分析表:
平均分 | 方差 | 中位数 | 合格率 | 优秀率 | |
男生 | 6.9 | 2.4 | ______ | 91.7% | 16.7% |
女生 | ______ | 1.3 | ______ | 83.3% | 8.3% |
(2)男生说他们的合格率、优秀率均高于女生,所以他们的成绩好于女生,但女生不同意男生的说法,认为女生的成绩要好于男生,请给出两条支持女生观点的理由;
(3)体育老师说,咱班的合格率基本达标,但优秀率太低,我们必须加强体育锻炼,两周后的目标是:全班优秀率达到50%.如果女生新增优秀人数恰好是男生新增优秀人数的两倍,那么男、女生分别新增多少优秀人数才能达到老师的目标?
【题目】小丽购买学习用品的收据如表,因污损导致部分数据无法识别,根据下表,解决下列问题:
(1)小丽买了自动铅笔、记号笔各几支?
(2)若小丽再次购买软皮笔记本和自动铅笔两种文具,共花费15元,则有哪几种不同的购买方案?
商品名 | 单价(元) | 数量(个) | 金额(元) |
签字笔 | 3 | 2 | 6 |
自动铅笔 | 1.5 | ● | ● |
记号笔 | 4 | ● | ● |
软皮笔记本 | ● | 2 | 9 |
圆规 | 3.5 | 1 | ● |
合计 | 8 | 28 |