题目内容
【题目】已知:在Rt△ABC中,∠B=90°,∠ACB=30°,点D为BC边上一动点,以AD为边,在AD的右侧作等边三角形ADE.
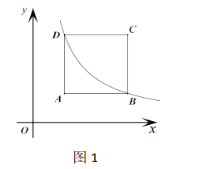
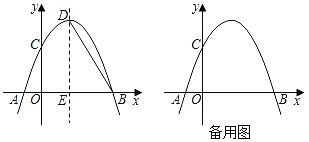
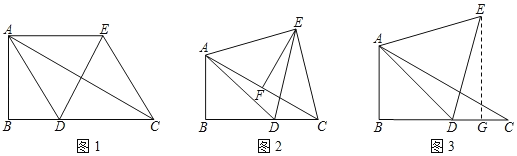
(1)当AD平分∠BAC时,如图1,四边形ADCE是 形;
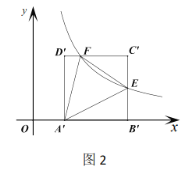
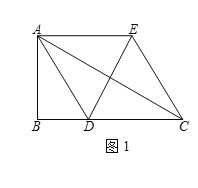
(2)过E作EF⊥AC于F,如图2,求证:F为AC的中点;
(3)若AB=2,
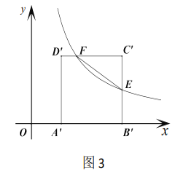
①当D为BC的中点时,过点E作EG⊥BC于G,如图3,求EG的长;
②点D从B点运动到C点,则点E所经过路径长为 .(直接写出结果)
【答案】(1)菱形;(2)证明见解析;(3)①EG![]() ;②2
;②2![]() .
.
【解析】
(1)根据平行四边形的判定定理得到四边形ADCE为平行四边形,证明AD=AE,根据菱形的判定定理证明结论;
(2)证明△BAD≌△FAE,根据全等三角形的性质得到AB=AF,根据直角三角形的性质得到AC=2AB,证明结论;
(3)①作EF⊥AC于F,连接EC,根据勾股定理求出BC,根据等腰三角形的性质求出CG,根据勾股定理计算,得到答案; ②根据线段垂直平分线的判定定理得到E'E'垂直平分AC,证明△E'AE'≌△BAC,得到E'E'=BC=![]() .
.
解:(1)在Rt△ABC中,∠B=90°,∠ACB=30°,
∴∠BAC=60°.
∵AD平分∠BAC,
∴∠BAD=∠DAC=30°.
∵△ADE为等边三角形,
∴∠DAE=60°,
∴∠EAC=30°,
∴∠EAC=∠ACB,∠DAC=∠ACB,
∴AE∥DC,AD=DC.
∵AE=AD,∴AE=CD,
∴四边形ADCE为平行四边形.
∵AD=AE,
∴平行四边形ADCE为菱形.
故答案为:菱形;
(2)![]()
![]()
在△BAD和△FAE中,
 ,
,
∴△BAD≌△FAE(AAS),
∴AB=AF,
在Rt△ABC中,∠B=90°,∠ACB=30°,
∴AC=2AB,
∴AC=2AF,
∴F为AC的中点;
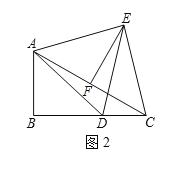
(3)①如图3,作EF⊥AC于F,连接EC,
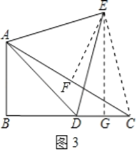
在Rt△ABC中,∠B=90°,∠ACB=30°,
∴AC=2AB=4,
∴BC![]() 2
2![]() ,
,
∵D为BC的中点,
∴BD![]() BC
BC![]() ,
,
∴AD![]() ,
,
∵AF=FC,EF⊥AC,
∴EC=AE=AD![]() ,
,
∵EC=EA=ED,EG⊥DC,
∴CG![]() CD
CD![]() ,
,
∴EG![]() ;
;
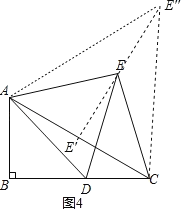
②如图4,当点D与点B重合时,点E在E'处,点E'是AC中点;
当点D与点C重合时,点E在E'处,其中△ACE'是等边三角形,
由(1)得:AE=CE,∴点E始终落在线段AC的垂直平分线上,
∴E'E'垂直平分AC,
∴点E的运动路径是从AC的中点E',沿着AC垂直平分线运动到E'处,
在△E'AE'和△BAC中,
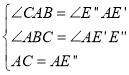 ,
,
∴△E'AE'≌△BAC(AAS),
∴E'E'=BC=2![]() .
.
故答案为:2![]() .
.