题目内容
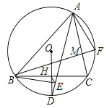
【题目】张老师给爱好学习的小军和小俊提出这样一个问题:如图①,在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.
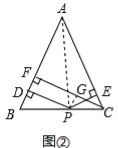
小军的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
小俊的证明思路是:如图2,过点P作PG⊥CF,垂足为G,可以证得:PD=GF,PE=CG,则PD+PE=CF.

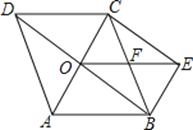
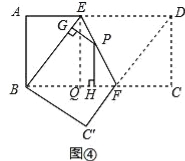
【变式探究】如图③,当点P在BC延长线上时,其余条件不变,求证:PD﹣PE=CF;请运用上述解答中所积累的经验和方法完成下题:
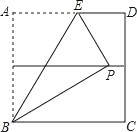
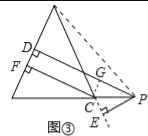
【结论运用】如图④,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值.
【答案】见解析.
【解析】
试题分析:证明:(方法1)连接AP,如图②∵PD⊥AB,PE⊥AC,CF⊥AB,且S△ABC=S△ABP+S△ACP,∴![]() ABCF=
ABCF=![]() ABPD+
ABPD+![]() ACPE,∵AB=AC,∴CF=PD+PE;
ACPE,∵AB=AC,∴CF=PD+PE;
(方法2)过点P作PG⊥CF,垂足为G,如图②,∵PD⊥AB,CF⊥AB,PG⊥FC,∴∠CFD=∠FDP=∠FGP=90°,∴四边形PDFG是矩形,∴DP=FG,∠DPG=90°,∴∠CGP=90°,∵PE⊥AC,∴∠CEP=90°,∴∠PGC=∠CEP,∵∠BDP=∠DPG=90°,∴PG∥AB,∴∠GPC=∠B,∵AB=AC,∴∠B=∠ACB,∴∠GPC=∠ECP,在△PGC和△CEP中,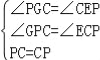 ,∴△PGC≌△CEP,∴CG=PE,∴CF=CG+FG=PE+PD;
,∴△PGC≌△CEP,∴CG=PE,∴CF=CG+FG=PE+PD;
【变式探究】证明:连接AP,如图③,∵PD⊥AB,PE⊥AC,CF⊥AB,且S△ABC=S△ABP﹣S△ACP,∴![]() ABCF=
ABCF=![]() ABPD﹣
ABPD﹣![]() ACPE,∵AB=AC,∴CF=PD﹣PE;
ACPE,∵AB=AC,∴CF=PD﹣PE;
【结论运用】过点E作EQ⊥BC,垂足为Q,如图④,∵四边形ABCD是矩形,∴AD=BC,∠C=∠ADC=90°,∵AD=8,CF=3,∴BF=BC﹣CF=AD﹣CF=5,由折叠可得:DF=BF,∠BEF=∠DEF,∴DF=5,∵∠C=90°,∴DC=![]() =4,∵EQ⊥BC,∠C=∠ADC=90°,∴∠EQC=90°=∠C=∠ADC,∴四边形EQCD是矩形,∴EQ=DC=4,∵AD∥BC,∴∠DEF=∠EFB,∵∠BEF=∠DEF,∴∠BEF=∠EFB,∴BE=BF,由问题情境中的结论可得:PG+PH=EQ,∴PG+PH=4,∴PG+PH的值为4.
=4,∵EQ⊥BC,∠C=∠ADC=90°,∴∠EQC=90°=∠C=∠ADC,∴四边形EQCD是矩形,∴EQ=DC=4,∵AD∥BC,∴∠DEF=∠EFB,∵∠BEF=∠DEF,∴∠BEF=∠EFB,∴BE=BF,由问题情境中的结论可得:PG+PH=EQ,∴PG+PH=4,∴PG+PH的值为4.

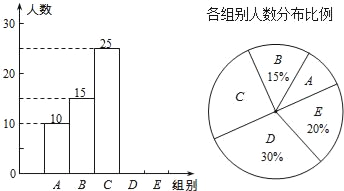
【题目】某校举行全体学生“汉字听写”比赛,每位学生听写汉字39个.随机抽取了部分学生的听写结果,绘制成如下的图表.
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息完成下列问题:
(1)统计表中的m= ,n= ,并补全条形统计图;
(2)扇形统计图中“C组”所对应的圆心角的度数是 ;
(3)已知该校共有900名学生,如果听写正确的字的个数少于24个定为不合格,请你估计该校本次听写比赛不合格的学生人数.