Question

【题目】如图所示：△ABC是等腰直角三角形，BC=AC，直角顶点C在x轴上，一锐角顶点B在y轴上

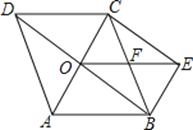
(1)如图1所示，若C的坐标是(2，0)，点A的坐标是(﹣2，﹣2)，求点B的坐标.

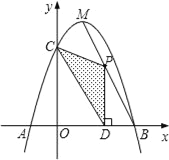
(2)如图2，若y轴恰好平分∠ABC，AC与y轴交于点D，过点A作AE⊥y轴 于E，求证：BD = 2AE

Answer 1

【答案】(1)B(0，4)；(2)证明见解析.

【解析】

（1）过点A作AD⊥OC，可证△ADC≌△COB，根据全等三角形对应边相等即可解题；

（2）延长BC，AE交于点F，可证△ACF≌△BCD，△ABE≌△FBE，即可求得BD=2AE．

（1）过点A作AD垂直OC于D．

∵∠DAC+∠ACD=90°，∠ACD+∠BCD=90°，

∴∠BCD=∠DAC．

在△ADC和△COB中，

∵，

∴△ADC≌△COB（AAS），

∴AD=OC，CD=OB．

∵A（-2，-2），C（2，0），

∴OD=2，OC=2，

∴OB=CD=2+2=4，

∴点B坐标为（0，4）；

（2）延长BC，AE交于点F．

∵AC=BC，AC⊥BC，∴∠BAC=∠ABC=45°．

∵BD平分∠ABC，

∴∠CBD=∠ABD=∠ABC=22.5°，∠DAE=90°﹣∠ABD﹣∠BAC=22.5°，

∴∠DAE=∠CBD=∠CAF．

在△ACF和△BCD中，

∵，

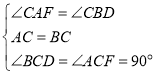∴△ACF≌△BCD（ASA），∴AF=BD，

在△ABE和△FBE中，

∵，

∴△ABE≌△FBE（ASA），

∴AE=EF，

∴BD=2AE．