题目内容
【题目】等腰三角形一腰上的高与底边的夹角为20°,则此三角形的顶角度数为_____.
【答案】40°.
【解析】
此题要分两种情况讨论:
(1)当等腰三角形的顶角是钝角时,腰上的高在三角形的外部,求出底角,再计算出顶角不是钝角,推出矛盾可知此情况不存在;
(2)当等腰三角形的顶角是锐角时,根据直角三角形的两个锐角互余,求得底角,再根据三角形的内角和是180°,可得顶角的度数.
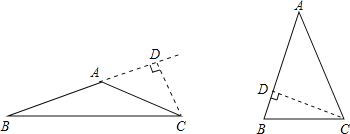
解:如图,分两种情况讨论:
(1)顶角是钝角时,由题意得:∠B=90°﹣20°=70°,
∴顶角=180°﹣2×70°=40°,不是钝角,故此情况不存在;
(2)顶角是锐角时,∠B=90°﹣20°=70°,
∠A=180°﹣2×70°=40°,是锐角,符合题意.
故答案为:40°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】为降低空气污染,公交公司决定全部更换节能环保的燃气公交车.计划购买A型和B型两种公交车共10辆,其中每台的价格,年均载客量如表:
A型 | B型 | |
价格(万元/辆) | a | b |
年均载客量(万人/年/辆) | 60 | 100 |
若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元
(1)求购买每辆A型公交车和每辆B型公交车分别多少万元?
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车年均载客总和不少于680万人次,有哪几种购车方案?请你设计一个方案,使得购车总费用最少.