Question

【题目】边长为4的正方形ABCD中，点E是BC边上的一个动点，连接DE，交AC于点N，过点D作DF⊥DE，交BA的延长线于点F，连接EF，交AC于点M．

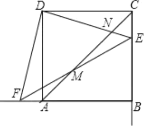
（1）判定△DFE的形状，并说明理由；

（2）设CE=x，△AMF的面积为y，求y与x之间的函数关系式；并求出当x为何值时y有最大值？最大值是多少？

Answer 1

【答案】（1）△DFE为等腰直角三角形，理由见解析；（2）当时，y有最大值1

【解析】

（1）先判断出∠FDA=∠CDE，证得△ADF≌△CDE，即可得出结论；
（2）分两种情况，利用平行线分线段成比例定理得出比例式表示出AF边上的高，即可得出结论；

（1）在正方形ABCD中，AD=CD，∠ADC=∠DCB=∠DAB =90°，

∵∠FDE=∠ADC=90°，

∴∠ADF+∠ADE =∠CDE+∠ADE=90°，

∴∠ADF=∠CDE，

在△ADF和△CDE中，

，

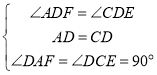∴△ADF≌△CDE，

∴DF=DE，

∴△DFE为等腰直角三角形；

（2）过M作MG⊥AB于G，

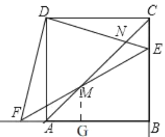
设MG=h，

又∵∠GAM =45°，

∴AG =MG=h，由（1）知FA=CE =，

∵CB⊥AB，

∴MG//BC，

∴，即，

∴h=，

∴；

即，

∵，

∴当时，有最大值1；