题目内容
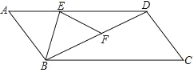
【题目】.E为□ABCD边AD上一点,将ABE沿BE翻折得到FBE,点F在BD上,且EF=DF.若∠C=52°,则∠ABE=____.
【答案】51°
【解析】
由平行四边形的性质和折叠的性质得出∠BFE=∠A=52°,∠FBE=∠ABE,由等腰三角形的性质和三角形的外角性质得出∠EDF=∠DEF=![]() ∠BFE=26°,由三角形内角和定理求出∠ABD=102°,即可得出∠ABE的度数.
∠BFE=26°,由三角形内角和定理求出∠ABD=102°,即可得出∠ABE的度数.
∵四边形ABCD为平行四边形,
∴∠A=∠C=52°,AD∥BC.
由折叠的性质可得∠ABE=∠FBE,∠A=∠BFE=52°,
∵EF=DF,
∴∠FED=∠EDF,
∴∠EFB=∠FED+∠EDF=2∠EDF=52°,即∠EDF=26°.
∵AD∥BC,
∴∠CBD=∠EDF=26°,∠ABC=180°-∠A=128°,
∴∠ABF=∠ABC-∠CBD=128°-26°=102°.
又∵∠ABE=∠FBE,
∴∠ABE=![]() ∠ABF=
∠ABF= ![]() ×102°=51°.
×102°=51°.

练习册系列答案
相关题目