题目内容
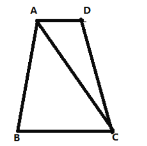
【题目】如图所示,![]() 是
是![]() 的外接圆,
的外接圆,![]() 为直径,
为直径,![]() 的平分线交O于点D,过点D作
的平分线交O于点D,过点D作![]() ,分别交
,分别交![]() ,
,![]() 的延长线于点E,F.
的延长线于点E,F.
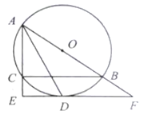
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)填空:
①当![]() 的度数为_________时,四边形
的度数为_________时,四边形![]() 为菱形;
为菱形;
②若![]() 的半径为
的半径为![]() ,
,![]() ,则
,则![]() 的长为_________.
的长为_________.
【答案】(1)见解析;(2)①60°;②4
【解析】
(1)连接OD,证OD∥AE,从而得出OD⊥EF,从而证切线;
(2)①当∠BAC=60°时,可得到AC=OD,又根据AC∥OD,可得四边形ACDO是平行四边形,根据AO=OD,可得平行四边形ACDO是菱形;
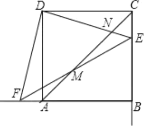
②如下图,设CE=x,则AC=3x,先证△OGB∽△ACB,得出OG=![]() ,再利用OG+CE=OD推导得出x的值,最后在Rt△OGB中,求得GB的长,进而得出CB的长.
,再利用OG+CE=OD推导得出x的值,最后在Rt△OGB中,求得GB的长,进而得出CB的长.
(1)如下图,连接OD
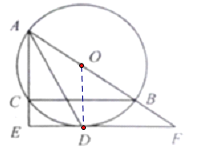
∵AO=OD,∴∠OAD=∠ODA
∵AD是∠EAB的角平分线,∴∠EAD=∠DAO
∴∠ADO=∠EAD
∴AE∥OD
∵AE⊥EF
∴OD⊥EF
∴![]() 是
是![]() 的切线;
的切线;
(2)①当∠BAC=60°时,四边形ACDO是菱形
如下图,连接CD
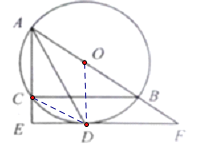
∵AB是![]() 的直径,∴∠ACB=90°
的直径,∴∠ACB=90°
∵∠CAB=60°
∴∠ABC=30°
∴在Rt△ABC中,AC=![]() ,即AC=AO=OB
,即AC=AO=OB
∵AO=OD
∴AC=OD
∵AC∥OD,∴四边形ACDO是平行四边形
∵AO=OD
∴平行四边形ACDO是菱形;
②如下图,OD与AB交于点G

设CE=x,则AC=3x
∵OD∥AE,∠ACB=90°
∴∠OGB=∠ACB=90°
∴根据垂径定理,CG=GB
∵∠OBG=∠ABC
∴△OBG∽△ABC
∴![]() ,∴OG=
,∴OG=![]()
∵OD=OG+GD=OG+CE,∴OD=![]() =
=![]()
∴x=1
∴在Rt△OGB中,OB=![]() ,OG=
,OG=![]() ,则GB=2
,则GB=2
∴CG=2,CB=4.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目