题目内容
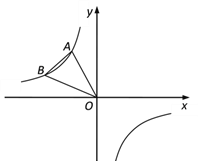
【题目】如图,点A、B在反比例函数y=- ![]() 的图象上,且点A、B的横坐标分别为a、2a(a<0).
的图象上,且点A、B的横坐标分别为a、2a(a<0).
(1)求△AOB的面积;
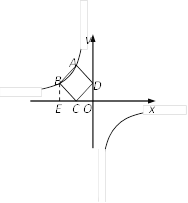
(2)若点C在x轴上,点D在y轴上,且四边形ABCD为正方形,求a的值.
【答案】(1)3;(2)a=- ![]()
【解析】试题分析:![]() 作AM⊥x轴于M,BN⊥x轴于N,设AM交OB于点E, S△AOM =S△BON, S△AOE =S梯形BEMN ,得到S△AOB =S梯形BAMN,求出梯形的面积即可.
作AM⊥x轴于M,BN⊥x轴于N,设AM交OB于点E, S△AOM =S△BON, S△AOE =S梯形BEMN ,得到S△AOB =S梯形BAMN,求出梯形的面积即可.
![]() 作BE⊥x轴于E,证明Rt△EBC≌Rt△OCD,
作BE⊥x轴于E,证明Rt△EBC≌Rt△OCD,![]()
列出式子![]() 求解即可.
求解即可.
试题解析:![]() 作AM⊥x轴于M,BN⊥x轴于N,设AM交OB于点E,
作AM⊥x轴于M,BN⊥x轴于N,设AM交OB于点E,
则S△AOM =S△BON,
∴S△AOE =S梯形BEMN ,∴S△AOB =S梯形BAMN
由题意知,![]()
![]()
![]()
(2)作BE⊥x轴于E,
∵四边形ABCD为正方形,∴BC=CD,∠BCD=90°,
∴∠BCE+∠OCD=90°,
又∠BCE+∠EBC=90°,∴∠EBC=∠OCD,
∴Rt△EBC≌Rt△OCD,
∴BE=CO,
又![]() 点C在x轴上,点D在y轴上
点C在x轴上,点D在y轴上
![]()
![]()


练习册系列答案
相关题目