题目内容
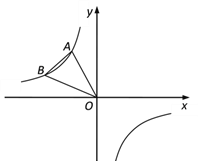
【题目】如图,在平面直角坐标系xOy中,直线y=kx(k≠0)沿着y轴向上平移3个单位长度后,与x轴交于点B(3,0),与y轴交于点C,抛物线y=x2+bx+c过点B、C且与x轴的另一个交点为A.
(1)求直线BC及该抛物线的表达式;
(2)设该抛物线的顶点为D,求△DBC的面积;
(3)如果点F在y轴上,且∠CDF=45°,求点F的坐标.
【答案】(1)抛物线的解析式为y=x2﹣4x+3;(2)S△DBC=3;(3)F(0,﹣![]() ).
).
【解析】试题分析:
(1)由题意可设平移后的直线的解析式为y=kx+3,代入点B的坐标可求得k的值,从而可得直线BC的解析式y=-x+3,由此可解得点C的坐标,将B、C的坐标代入抛物线的解析式列方程组可求得b、c的值,即可得到抛物线的解析式;
(2)如图1所示:过点C作CE∥x轴,过点B作EF∥y轴,过点D作DF∥x轴,由(1)中所得抛物线的解析式求出其顶点D的坐标即可由S△DBC=S四边形CEFG﹣S△CDG﹣S△BFD﹣S△BCE求出其面积了;
(3)如图2所示:过点F作FG⊥CD,垂足为G.由(1)(2)易得CD=![]() ,tan∠OCD=tan∠GCF=
,tan∠OCD=tan∠GCF=![]() ,则CG=2FG,由∠GCF=45°,∠FGD=90°可得△FGD为等腰直角三角形,由此可得FG=GD,由此可得CD=3FG,则FG=
,则CG=2FG,由∠GCF=45°,∠FGD=90°可得△FGD为等腰直角三角形,由此可得FG=GD,由此可得CD=3FG,则FG=![]() ,CG=
,CG=![]() ,从而在Rt△CFG中,可得CF=
,从而在Rt△CFG中,可得CF=![]() ,则OF=CF﹣OC=
,则OF=CF﹣OC=![]() ,就可得到点F的坐标为(0,﹣
,就可得到点F的坐标为(0,﹣![]() ).
).
试题解析:
(1)将直线y=kx(k≠0)沿着y轴向上平移3个单位长度,所得直线的解析式为y=kx+3,
将点B(3,0)代入得:3k+3=0,解得k=﹣1,
∴直线BC的解析式为y=﹣x+3.
令x=0得:y=3,
∴C(0,3).
将B(3,0),C(0,3)代入抛物线的解析式得:![]() ,解得:b=﹣4,c=3,
,解得:b=﹣4,c=3,
∴抛物线的解析式为y=x2﹣4x+3.
(2)如图1所示:过点C作CE∥x轴,过点B作EF∥y轴,过点D作DF∥x轴.
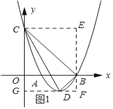
y=x2﹣4x+3=(x﹣2)2﹣1.
∴D(2,﹣1).
∴S△DBC=S四边形CEFG﹣S△CDG﹣S△BFD﹣S△BCE=12﹣![]() ×2×4﹣
×2×4﹣![]() ×1×1﹣
×1×1﹣![]() ×3×3=3.
×3×3=3.
(3)如图2所示:过点F作FG⊥CD,垂足为G,由(1)(2)易得CD=![]() ,
,
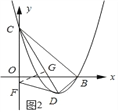
∵C(0,3),D(2,﹣1),
∴CD=![]() ,
,
∵tan∠OCD=tan∠GCF=![]() ,
,
∴CG=2FG.
又∵∠GCF=45°,∠FGD=90°,
∴△FGD为等腰直角三角形,
∴FG=GD.
∴CD=3FG,
∴FG=![]() .
.
∴CG=2FG=![]() .
.
∴在Rt△CFG中,依据勾股定理可知:CF=![]() .
.
∴OF=CF﹣OC=![]() .
.
∴F(0,﹣![]() ).
).

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案