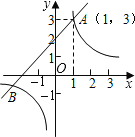��Ŀ����
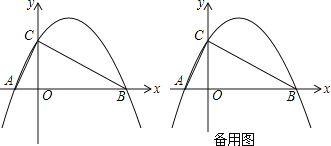
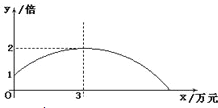
����Ŀ��ij��˾����һ�ֲ�Ʒ��ÿ����Ʒ�ijɱ��ۡ����ۼۼ��������������Ϊ�˻�ȡ���������˾����Ͷ��һ�����ʽ���������棬������֣�ÿ��Ͷ��Ĺ���Ϊx��Ԫ����Ʒ������������ԭ��������y������y��x�ĺ���ͼ��Ϊ��ͼ��ʾ��һ�������ߣ�
�ɱ��ۣ�Ԫ/���� | ���ۼۣ�Ԫ/���� | �����������/�£� |
2 | 3 | 9 |
��1����y��x�ĺ�����ϵʽΪ ���Ա���x��ȡֵ��ΧΪ ��
��2����֪������������ܶ��ȥ�ɱ��Ѻ��ѣ�Ҫʹÿ��������������ʹ�˾ӦͶ����ٹ��ѣ�
���𰸡���1��y=��![]() ��x��3��2+2��0��x��7.2����2��Ͷ��2.5����ѣ�
��x��3��2+2��0��x��7.2����2��Ͷ��2.5����ѣ�
��������
�����������1������������ͼ���ܹ�д��y��x�ĺ�����ϵʽ��Ȼ�����y=0ʱ��x��ֵ��
��2������������������ܶ��ȥ�ɱ��Ѻ��ѣ�д��������ϵʽ������������
�⣺��1����y��x�ĺ�����ϵʽΪy=a��x��b��2+c��
����ͼ���֪b=3��c=2��a=��![]() ��
��
��y=��![]() ��x��3��2+2��
��x��3��2+2��
��y=0�����x=7.2��
���Ա���x��ȡֵ��ΧΪ0��x��7.2��
��2����������������ܶ��ȥ�ɱ��Ѻ��ѣ����г�������ϵʽ
w=����x��3��2+18��x��
��w=��x2+5x+9��
��x=2.5ʱ���������
��Ͷ��2.5����ѣ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�