题目内容
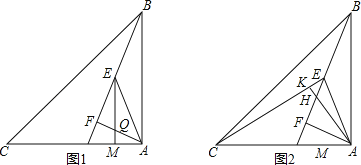
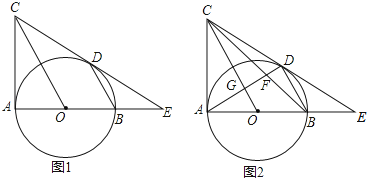
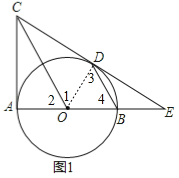
【题目】如图,∠BAC=90°,以AB为直径作⊙O,BD∥OC交⊙O于D点,CD与AB的延长线交于点E.
(1)求证:CD是⊙O的切线;
(2)若BE=2,DE=4,求CD的长;
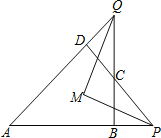
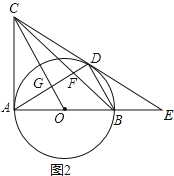
(3)在(2)的条件下,如图2,AD交BC、OC分别于F、G,求![]() 的值.
的值.
【答案】(1)见解析;(2)CD=6;(3)![]() .
.
【解析】
试题分析:(1)连接OD,如图1,利用平行线的性质得∠1=∠3,∠2=∠4,加上∠3=∠4,则∠1=∠2,于是可根据“SAS”判定△CDO≌△CAO,则∠CDO=∠CAO=90°,然后根据切线的判定定理可得到CD是⊙O的切线;
(2)设⊙O半径为r,则OD=OB=r,在Rt△ODE中利用勾股定理得到r2+42=(r+2)2,解得r=3,即OB=3,然后根据平行线分线段成比例定理,由DB∥OC得到DE:CD=BE:OB,于是可计算出CD=6;
(3)如图3,由△CDO≌△CAO得到AC=CD=6,在Rt△AOC中利用勾股定理计算出OC=3![]() ,再证明Rt△OAG∽△OCA,利用相似比计算出OG=
,再证明Rt△OAG∽△OCA,利用相似比计算出OG=![]() ,则CG=OC﹣OG=
,则CG=OC﹣OG=![]() ,易得BD=2OG=
,易得BD=2OG=![]() ,然后利用CG∥BD得到
,然后利用CG∥BD得到![]() =
=![]() =
=![]() .
.
(1)证明:连接OD,如图1,
∵BD∥OC,
∴∠1=∠3,∠2=∠4,
又∵OD=OB,
∴∠3=∠4,
∴∠1=∠2,
在△CAO和△CDO中,
 ,
,
∴△CDO≌△CAO,
∴∠CDO=∠CAO=90°,
∴CD⊥OD,
∴CD是⊙O的切线;
(2)解:设⊙O半径为r,则OD=OB=r,
在Rt△ODE中,∵OD2+DE2=OE2,
∴r2+42=(r+2)2,解得r=3,
∴OB=3,
∵DB∥OC,
∴DE:CD=BE:OB,即4:CD=2:3,
∴CD=6;
(3)解:如图3,
由(1)得△CDO≌△CAO,
∴AC=CD=6,
在Rt△AOC中,OC=![]() =
=![]() =3
=3![]() ,
,
∵∠AOG=∠COA,
∴Rt△OAG∽△OCA,
∴OA:OC=OG:OA,即3:3![]() =OG:3,
=OG:3,
∴OG=![]() ,
,
∴CG=OC﹣OG=3![]() ﹣
﹣![]() =
=![]() ,
,
∵OG∥BD,OA=OB,
∴OG为△ABD的中位线,
∴BD=2OG=![]() ,
,
∵CG∥BD,
∴![]() =
=![]() =
=![]() =
=![]() .
.

 口算题天天练系列答案
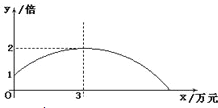
口算题天天练系列答案【题目】某公司销售一种产品,每件产品的成本价、销售价及月销售量如表;为了获取更大的利润,公司决定投入一定的资金做促销广告,结果发现:每月投入的广告费为x万元,产品的月销售量是原销售量的y倍,且y与x的函数图象为如图所示的一段抛物线.
成本价(元/件) | 销售价(元/件) | 销售量(万件/月) |
2 | 3 | 9 |
(1)求y与x的函数关系式为 ,自变量x的取值范围为 ;
(2)已知利润等于销售总额减去成本费和广告费,要使每月销售利润最大,问公司应投入多少广告费?