题目内容
【题目】如图，已知一次函数y1=x+m（m为常数）的图象与反比例函数
（k为常数，k≠0）的图象相交点A（1，3）．
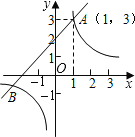
（1）求这两个函数的解析式及其图象的另一交点B的坐标；
（2）观察图象，写出使函数值y1≥y2的自变量x的取值范围．
【答案】（1）y1=x+2．y2=
．B（﹣3，﹣1）．（2）当﹣3≤x＜0或x≥1时，函数值y1≥y2．
【解析】
试题分析：（1）一次函数和反比例函数都是一个未知字母，把交点代入函数解析式即可；再根据求得的解析式进一步求得另一个交点的坐标即可．
（2）应从交点处看在交点的哪一边一次函数的函数值＞反比例函数的函数值．
解：（1）由题意，得3=1+m，
解得：m=2．
所以一次函数的解析式为y1=x+2．
由题意，得3=
，
解得：k=3．
所以反比例函数的解析式为y2=．
由题意，得x+2=，
解得x1=1，x2=﹣3．
当x2=﹣3时，y1=y2=﹣1，
所以交点B（﹣3，﹣1）．
（2）由图象可知，当﹣3≤x＜0或x≥1时，函数值y1≥y2．
练习册系列答案
相关题目
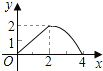
【题目】某公司销售一种产品，每件产品的成本价、销售价及月销售量如表；为了获取更大的利润，公司决定投入一定的资金做促销广告，结果发现：每月投入的广告费为x万元，产品的月销售量是原销售量的y倍，且y与x的函数图象为如图所示的一段抛物线．
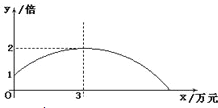
成本价（元/件） | 销售价（元/件） | 销售量（万件/月） |
2 | 3 | 9 |
（1）求y与x的函数关系式为 ，自变量x的取值范围为 ；
（2）已知利润等于销售总额减去成本费和广告费，要使每月销售利润最大，问公司应投入多少广告费？
