题目内容
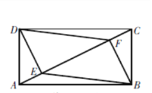
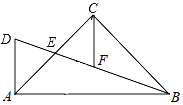
【题目】如图,四边形ABCD内接于⊙O,F是 ![]() 上一点,且
上一点,且 ![]() =
= ![]() ,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=30°,则∠E的度数为( )
,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=30°,则∠E的度数为( ) 
A.45°
B.50°
C.55°
D.60°
【答案】A
【解析】解:∵四边形ABCD内接于⊙O,∠ABC=105°, ∴∠ADC=180°﹣∠ABC=180°﹣105°=75°.
∵ ![]() =
= ![]() ,∠BAC=30°,
,∠BAC=30°,
∴∠DCE=∠BAC=30°,
∴∠E=∠ADC﹣∠DCE=75°﹣30°=45°.
故选A.
【考点精析】通过灵活运用圆心角、弧、弦的关系和圆内接四边形的性质,掌握在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形即可以解答此题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
【题目】目前,我国大约有1.3亿高血压病患者,预防高血压不容忽视,“千帕![]() ”和“毫米汞柱
”和“毫米汞柱![]() ”都是表示血压的单位,请你根据表格提供的信息判断,下列各组换算正确的是( )
”都是表示血压的单位,请你根据表格提供的信息判断,下列各组换算正确的是( )
千帕 | … | 10 | 12 | 14 | … |
毫米汞柱 | … | 75 | 90 | 105 | … |
A.![]() B.
B.![]()
C.![]() D.
D.![]()