Question

【题目】如图，一块长方形场地ABCD的长AB与宽AD的比为2∶1，DE⊥AC于点E，BF⊥AC于点F，连结BE，DF，则四边形DEBF与长方形ABCD的面积比为__________.

Answer 1

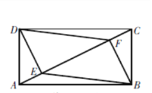
【答案】3∶5

【解析】

根据题意可设AD=x，则AB=2x，AC=x，利用△ADC的面积为定值可求DE的长，再根据勾股定理可求出AE，EF，CF的长，再分别计算出四边形DEBF与矩形ABCD的面积，再作比值即可．

在矩形ABCD中，∠ADC=90°，设AD=x，则AB=AB=2x，AC=x，

∵DE⊥AC于点E，

∴DE==，

在△ADE中，AE==，同理CF=，EF=x，

∴ S四边形DEBF=EF×DE=x= x2，

而S矩形ABCD=x×2x=2x2，

∴四边形DEBF与矩形ABCD的面积之比为 x2：2x2=3：5,

故答案为3：5.