题目内容
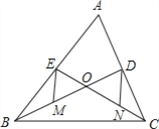
【题目】如图,已知△ABC的中线BD、CE相交于点O、M、N分别为OB、OC的中点.
(1)求证:MD和NE互相平分;
(2)若BD⊥AC,EM=2![]() ,OD+CD=7,求△OCB的面积.
,OD+CD=7,求△OCB的面积.
【答案】(1)见试题解析(2)8.5.
【解析】试题分析:(1)连接ED、MN,根据三角形中位线定理可得ED∥MN,ED=MN,进而得到四边形DEMN是平行四边形,再根据平行四边形的性质可得MD和NE互相平分;
(2)利用(1)中所求得出OC=2DN=4![]() ,再利用勾股定理以及三角形面积公式求出S△OCB=
,再利用勾股定理以及三角形面积公式求出S△OCB=![]() OB×CD即可.
OB×CD即可.
试题解析:(1)证明:连接ED、MN,
∵CE、BD是△ABC的中线,
∴E、D是AB、AC中点,
∴ED∥BC,ED=![]() BC,
BC,
∵M、N分别为OB、OC的中点,
∴MN∥BC,MN=![]() BC,
BC,
∴ED∥MN,ED=MN,
∴四边形DEMN是平行四边形,
∴MD和NE互相平分;
(2)解:由(1)可得DN=EM=2![]() ,
,
∵BD⊥AC,
∴∠ODC=90°,
∵N是OC的中点,
∴OC=2DN=4![]() (直角三角形斜边中线等于斜边的一半)
(直角三角形斜边中线等于斜边的一半)
∵OD2+CD2=OC2=32,
(OD+CD)2=OD2+CD2+2OD×CD=72=49,
2OD×CD=49﹣32=17,
OD×CD=8.5,
∵OB=2OM=2OD,
∴S△OCB=![]() OB×CD=OD×CD=8.5.
OB×CD=OD×CD=8.5.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目